Zjednodušený bilanční výpočet ročních přínosů fotovoltaických instalací
Výpočet produkce elektrické energie fotovoltaickými systémy lze provést více či méně zjednodušeným způsobem. Měsíční bilanční metoda umožňuje do výpočtu měsíční produkce zahrnout vliv teploty a slunečního ozáření s využitím parametrů uváděných v technické specifikaci fotovoltaických modulů. Jednotlivé technologie FV modulů jsou bilančním výpočtem porovnány.
Úvod
Projektanti, kteří navrhují technologie do budov, a energetičtí specialisté, kteří budovy posuzují v rámci energetického hodnocení, potřebují na jedné straně jednoduché výpočetní nástroje pro hodnocení přínosu systémů využívajících obnovitelné zdroje energie v daných aplikacích, nicméně na straně druhé potřebují výpočetní nástroje dostatečně spolehlivé a zohledňující konkrétní použité prvky. Používání komplexních simulačních modelů pro výpočtové hodnocení systémů není v praxi časté a pro konvenční systémy ani nedává smysl.
V ČR je v rámci souboru norem pro energetické hodnocení budov zavedena norma ČSN EN 15316-4-6 [1], která stanovuje roční produkci elektrické energie fotovoltaickým systémem pouze na základě jeho špičkového výkonu bez ohledu na reálné provozní vlivy pro konkrétní použité fotovoltaické moduly a další prvky systému.
V textu příspěvku je navržen postup výpočtu produkce elektrické energie fotovoltaickým systémem, metodologicky podobný zavedenému výpočtovému postupu pro bilancování energetických zisků solární tepelné soustavy [2], avšak přizpůsobený specifickým vlastnostem FV systémů. Postup umožňuje zohlednit vliv teploty FV článku a vliv úrovně slunečního ozáření během roku na účinnost modulů na základě údajů uvedených v jejich technické specifikaci od výrobce. Postup uvažuje i elektrické ztráty na DC a AC vedení a ztráty měniče. Oproti výpočtovému postupu v [1] jsou navíc výsledkem údaje o měsíční produkci elektrické energie, ne pouze jediná celoroční hodnota. Postup využívá sjednocené klimatické údaje, definované v TNI 73 0331 [3] pro hodnocení energetické náročnosti budov. Oba uvedené postupy řeší pouze produkci elektrické energie bez jejího využití, případně akumulace.
Postup podle ČSN EN 15316-4-6
Prvním úskalím evropské normy je její název „Výroba tepla, fotovoltaické soustavy“. Není potřeba připomínat, že cílem fotovoltaických systémů není výroba tepla, ale elektrické energie pro využití v budově nebo v rozvodné síti pro krytí potřeby elektrické energie. Výpočet neuvažuje systémy s akumulací elektrické energie. V následujícím textu je značení používané v normě upraveno pro sjednocení značení v celém textu, původní značení je však uvedeno.
| Druh fotovoltaického modulu | Kpk [kW/m2] |
|---|---|
| Monokrystalický křemík | 0,12 až 0,18 |
| Multikrystalický křemík | 0,10 až 0,16 |
| Tenkovrstvý amorfní křemík | 0,04 až 0,08 |
| Ostatní tenkovrstvé | 0,035 |
| Tenkovrstvý CIGS (měď-indium-galium-diselenid) | 0,105 |
| Tenkovrstvý CdTe (kadmium-telurid) | 0,095 |
Elektrická energie dodaná fotovoltaickým systémem EFV,sys [kWh/rok], v [1] označená jako Eel,pv,out, se stanoví jako
kde je
- HT,rok
- roční dávka slunečního ozáření [kWh/m2.rok] dopadající na fotovoltaický systém, v [1] označená jako Esol,
- Ppk
- špičkový výkon FV systému [kW],
- fperf
- činitel výkonnosti fotovoltaického systému [–],
- Gref
- referenční sluneční ozáření, v [1] označené jako Iref, rovné 1 kW/m2.
Špičkový výkon fotovoltaického systému Ppk se získá z parametrů FV pole za normových zkušebních podmínek (referenční zkušební hodnoty teploty článku 25 °C, ozáření v rovině Gref = 1 kW/m2, referenční sluneční spektrum AM 1,5 při zkoušce FV modulu).
Pokud Ppk [kW] není k dispozici, může být vypočten orientačně podle vztahu
kde je
- Kpk
- součinitel špičkového výkonu [kW/m2] závisející na druhu technologie fotovoltaického modulu (informativní hodnoty jsou uvedeny v tab. 1, u krystalických technologií se uvažuje minimální faktor zaplnění apertury články 80 %),
- AFV
- celková činná plocha [m2] všech fotovoltaických modulů (bez rámu), v [1] označená jako A.
Při bližším pohledu není součinitel špičkového výkonu ničím jiným než referenční účinností FV modulu.
Činitel výkonnosti systému fperf zohledňuje výkonnost fotovoltaické instalace integrované do budovy v závislosti na:
- soustavě přeměny ze stejnosměrného proudu na střídavý proud (paušálně),
- skutečné provozní teplotě fotovoltaických modulů (paušálně),
- integraci fotovoltaických modulů do budovy (rozlišeno v tab. 2).
Rozlišení mezi různými druhy integrace do budovy je provedeno podle způsobu větrání fotovoltaických modulů. Informativní hodnoty činitele výkonnosti systému fperf jsou uvedeny v tab. 2.
| Druh integrace fotovoltaického modulu do budovy | fperf [–] |
|---|---|
| Nevětrané moduly | 0,70 |
| Mírně větrané moduly | 0,75 |
| Silně větrané moduly nebo nuceně větrané moduly | 0,80 |
Zjednodušená bilanční metoda
Před vysvětlením vlastního principu bilanční metody je vhodné se nejprve podívat na vybrané parametry fotovoltaického modulu, které se použijí pro výpočet. Zjednodušená bilanční metoda nepracuje s voltampérovou charakteristikou jako podrobné matematické modely FV modulů. Pro výpočet se jako základní údaje využívají referenční účinnost modulů ηref [%], instalovaný špičkový výkon Ppk [kW], případně činná plocha FV modulů AFV [m2]. Pro zohlednění vlivu provozních podmínek na účinnost modulů je však nutné použít i další parametry ze specifikace výrobce, jako je teplotní výkonový součinitel γ [%/K], jmenovitá provozní teplota článku NOCT a pokles účinnosti s poklesem slunečního ozáření ΔηG [%].
Účinnost FV modulu závisí na teplotě FV článků. S rostoucí teplotou se účinnost FV modulu snižuje podle lineárního vztahu
kde je
- ηref
- referenční účinnost [%] při normových zkušebních podmínkách (1000 W/m2, 25 °C),
- tFV
- teplota fotovoltaického článku [°C],
- tref
- referenční teplota článku 25 °C,
- γ
- teplotní součinitel výkonu [%/K] pro daný modul.
Výrobce v podkladech k FV modulům uvádí výkonový teplotní součinitel γ jako procentní snížení výkonu modulu vztažené na 1 K zvýšení teploty oproti referenční teplotě článku. Hodnota součinitele γ je záporná.
Teplotu FV článku v provozu je možné zjistit s využitím tzv. jmenovité provozní teploty článku NOCT. Tu udává výrobce pro definované provozní podmínky, odlišné od normových zkušebních: sluneční ozáření G = 800 W/m2, teplota okolního vzduchu te = 20 °C, rychlost větru 1 m/s a stav bez odběru elektrické energie z FV článku (otevřený obvod).
Vlastní energetickou bilanci FV článku lze zjednodušeně popsat rovnicí
kde je
- α
- pohltivost FV modulu,
- ηFV
- elektrická účinnost FV modulu [%],
- G
- sluneční ozáření [W/m2],
- U
- celkový součinitel tepelné ztráty z FV článku do okolí [W/m2K], vyjadřující celkový tepelný tok z FV článku krycími vrstvami (laminační vrstva a sklo na přední straně, laminační vrstva a krycí elektroizolační vrstvy na zadní straně) a přestupem tepla z předního a zadního povrchu do okolí,
- tFV
- teplota FV článku [°C],
- te
- teplota okolního vzduchu [°C].
Pokud se energetická bilance zapíše pro podmínky NOCT (otevřený obvod, ηFV = 0), rovnice pro teplotu FV článku popisuje právě NOCT
Při uvažování pohltivosti modulu α = (1 − ρ), kde ρ je odrazivost modulu pohybující se při kolmém úhlu dopadu na úrovni cca 5 %, lze z rovnice (5) stanovit jedinou neznámou – součinitel tepelné ztráty z FV článku do okolí
Součinitel tepelné ztráty zohledňuje provedení vlastních modulů (tepelné odpory mezi FV článkem a oběma vnějšími povrchy modulu, přestup tepla z obou povrchů do okolí). Jmenovitá provozní teplota článku se u různých modulů a technologií pohybuje od zhruba 33 °C do 58 °C. Typická hodnota je okolo 45 °C.
Součinitel tepelné ztráty zahrnuje vliv přestupu tepla sáláním a vliv přestupu tepla prouděním (při výpočtu je uvažována rychlost proudění vzduchu 1 m/s). Při zjednodušujícím předpokladu, že podmínky sálání a proudění se během roku příliš nemění (jako např. při výpočtu součinitele prostupu tepla stavebních konstrukcí budov při výpočtu potřeby tepla), lze uvažovat součinitel U během roku konstantní a podle rovnice (7) určit pro každý měsíc střední teplotu FV článku při znalosti průměrných klimatických podmínek v daných měsících podle vztahu
kde je
- te,s
- střední denní teplota venkovního vzduchu v době slunečního svitu [°C],
- Gm
- střední sluneční ozáření [W/m2].
Účinnost FV modulů ηFV [%], která se zadává do vztahu (7), je zpětně závislá na teplotě tFV, která se ze vztahu vypočítá. Jedná se o použití iteračního řešení, ale pouze zdánlivě. Použití již iterované hodnoty účinnosti ηFV a použití referenční účinnosti ηref činí rozdíl ve výsledku teploty tFV desetiny K.
Účinnost FV modulu závisí obecně také na úrovni slunečního ozáření G. S výjimkou tenkovrstvých (např. CdTe) modulů se účinnost FV modulů s klesajícím slunečním ozářením snižuje přibližně logaritmicky podle vztahu
kde je
- ηref
- referenční účinnost [%] při normových zkušebních podmínkách,
- G
- sluneční ozáření pro stanovení poklesu účinnosti, zpravidla G = 200 W/m2,
- Gref
- referenční ozáření Gref = 1000 W/m2,
- k
- součinitel pro daný modul [–].
Výrobce v technické specifikaci k FV modulům zpravidla uvádí hodnotu relativního snížení účinnosti ΔηG z 1000 W/m2 na 200 W/m2. Hodnota ΔηG se uvádí jako záporná. Z této hodnoty je pak možné vyčíslit součinitel k podle vztahu
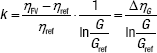 (9)
(9)
a s jeho pomocí pak přepočítat účinnost na jiné podmínky ozáření. Hodnota k se uvádí ve výpočtech jako kladná hodnota.
Celkovou měsíční účinnost modulu ηFV [%] lze stanovit použitím korigovaných účinností ze vztahů (3) a (8) jako
Úpravou a dosazením se získá komplexní rovnice pro měsíční účinnost na základě středních měsíčních hodnot klimatických údajů a parametrů modulu získaných z běžné technické specifikace výrobce
Měsíční produkci elektrické energie FV systémem EFV,sys [kWh/měs] lze stanovit na základě měsíčních klimatických podmínek a předpokládaných elektrických ztrát z celkové měsíční účinnosti FV modulu podle vztahu
kde je
- HT
- měsíční dávka slunečního ozáření [kWh/m2.měs],
- AFV
- činná plocha instalovaných FV modulů [m2],
- Ppk
- špičkový výkon instalovaných modulů [kW],
- ηFV
- měsíční účinnost modulů [%],
- ηref
- referenční účinnost modulů [%],
- Gref
- referenční sluneční ozáření rovné 1 kW/m2,
- p
- srážka vlivem elektrických ztrát [%].
Elektrické ztráty rozvodu v budově je možné zjednodušeně uvažovat následovně: ztráty na DC vedení 2 %, ztráty na měniči a sledovači výkonového maxima okolo 5 % a ztráty na AC vedení cca 1 %. Optické ztráty vlivem nekolmého úhlu dopadu slunečního záření během roku na FV moduly jsou v rovnici zohledněny konstantou 0,9.
Příklad výpočtu FV systému
V následujícím příkladu jsou vypočteny roční přínosy FV systému s vybranými zástupci jednotlivých technologií při stejné činné ploše modulů 10 m2. Systémové ztráty jsou uvažovány na úrovni 8 %. Parametry, které vstupují do výpočtu, jsou převzaty z technických listů konkrétních FV modulů a uvedeny souhrnně v tab. 3. Prezentované výsledky byly stanoveny výpočtem navrženou zjednodušenou bilanční metodou pro klimatické údaje v souladu s TNI 73 0331.
| Fotovoltaický modul | ηref [%] | γ [%/K] | NOCT [°C] | ΔηG [%] |
|---|---|---|---|---|
| Monokrystalický křemík (mono) | 15,9 | −0,44 | 44,7 | 4,0 |
| Polykrystalický křemík (poly) | 14,8 | −0,46 | 45,0 | 6,6 |
| Tenkovrstvý amorfní křemík (amo) | 8,5 | −0,24 | 46,0 | 2,6 |
| Tenkovrstvý CIGS | 12,6 | −0,38 | 51,0 | 4,0 |
| Tenkovrstvý CIS | 7,6 | −0,35 | 47,0 | 2,0 |
| HIT technologie | 19,0 | −0,30 | 44,0 | 0,9 |
V grafu na obr. 1 jsou uvedeny měsíční výsledky produkce elektrické energie celým FV systémem pro konkrétní technologii monokrystalických FV modulů o ploše 10 m2. Ve stejném grafu je zobrazen i průběh účinnosti samotných FV modulů během jednotlivých měsíců. Je patrné, že účinnost se během roku mění, v letním období je nejnižší s ohledem na vysokou provozní teplotu panelů. V zimním období je naopak účinnost nejvyšší.
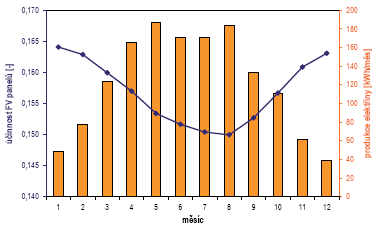
Obr. 1 Měsíční bilance FV systému s polykrystalickými moduly o ploše 10 m²
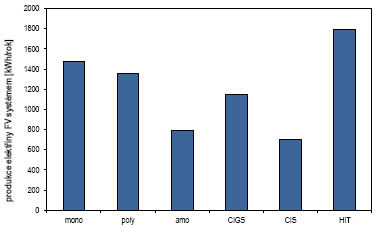
Obr. 2 Porovnání použití FV technologií
Na obr. 2 je srovnána roční produkce FV systému o ploše 10 m2 vybaveného různými fotovoltaickými technologiemi uvedenými v tab. 3. V tab. 4 jsou kromě roční produkce FV systému Esys uvedeny také jeho špičkový výkon Ppk, roční účinnost systému ηsys a také poměr celoroční účinnosti k referenční účinnosti použitého panelu dané FV technologie, což je ve své podstatě činitel výkonnosti systému fperf uváděný normou ČSN EN 15316-4-6.
| Fotovoltaický modul | Ppk [kW] | EFV,sys [kWh/rok] | ηsys [%] | fperf [–] |
|---|---|---|---|---|
| Monokrystalický křemík | 1,59 | 1471 | 12,8 | 0,81 |
| Polykrystalický křemík | 1,48 | 1351 | 11,8 | 0,80 |
| Tenkovrstvý amorfní křemík | 0,85 | 791 | 6,9 | 0,81 |
| Tenkovrstvý CIGS | 1,26 | 1149 | 10,0 | 0,80 |
| Tenkovrstvý CIS | 0,76 | 704 | 6,1 | 0,81 |
| HIT technologie | 1,90 | 1791 | 15,6 | 0,82 |
Z výsledků uvedených v tab. 4 je patrné, že činitel výkonnosti systému pro různé FV technologie se v podstatě pohybuje v rozmezí hodnot 0,80 až 0,82 při uvažování FV modulů na střeše budovy vystavených působení větru (silně větrané moduly). To jsou v podstatě shodné hodnoty s údajem uvedeným v tab. 2. Na rozdíl od výpočtu ČSN EN 15316-4-6 lze však zjednodušenou bilanční metodou stanovit jak měsíční produkci, tak měsíční účinnost konkrétního použitého modulu a případně zohlednit účinnosti či ztráty dalších prvků FV systému.
Závěr
Pro výpočet fotovoltaických systémů v rámci hodnocení energetické náročnosti budov je možné použít velmi jednoduchou metodu podle normy ČSN EN 15316-4-6. Metoda má řadu nevýhod a pro konkrétní FV systém s konkrétními FV moduly je vhodnější použít podrobnější výpočet na měsíční bázi, tzv. zjednodušenou bilanční metodu. Metoda byla použita pro porovnání měsíčního a ročního chování FV systému při použití jednotlivých technologií FV modulů. Výsledky potvrzují vhodnost ročního výpočtu podle normy, avšak zároveň ukazují možnost podrobnějšího srovnání technologií v měsíčním rozlišení, které je potřebné v případě hodnocení energetické náročnosti budov.
Odkazy
- [1] ČSN EN 15316-4-6 Tepelné soustavy v budovách – Výpočtová metoda pro stanovení energetických potřeb a účinností soustavy – Část 4-6: Výroba tepla, fotovoltaické soustavy. ÚNMZ 2014.
- [2] TNI 73 0302 Energetické hodnocení solárních tepelných soustav – Zjednodušený výpočtový postup. ÚNMZ 2014.
- [3] TNI 73 0331 Energetická náročnost budov – Typické hodnoty pro výpočet. ÚNMZ 2013.
Calculation of electricity production by photovoltaic systems can be performed by more or less simplified approach. Monthly balance method allows to include the influence of the temperature and solar irradiance into the monthly production calculation with use of the PV module parameters available in the technical datasheet. Individual PV module technologies are compared by the balance method.

VVI - odborný časopis Společnosti pro techniku prostředí určený především pro projektování a studium. Český odborný časopis pro techniku prostředí začal vycházet v roce 1958 pod názvem Zdravotní technika a vzduchotechnika (ZTV), v roce 1992 byl změněn ...