Vrt pro tepelné čerpadlo - model dlouhodobé energetické bilance - 1. část
Autor popisuje metodiku a výsledky matematického modelování transportu tepla v okolí vrtu pro tepelné čerpadlo. Na pozadí analyzovaného problému dukemntuje vybrané informace související s výskytem geotermální energie.
1 Úvod
Hlavním cílem předkládaného textu je čtenáře seznámit s metodikou a výsledky matematického modelování transportu tepla v okolí vrtu pro tepelné čerpadlo. Sekundárním cílem je na pozadí analyzovaného problému zdokumentovat vybrané informace související s výskytem geotermální energie se zaměřením na "mělkou geotermii", tedy vrty s hloubkou do cca 300 metrů.
2 Geotermální energie
Pojmem "geotermální energie" je možné v širším pojetí definovat jako teplo obsažené v zemském jádru a plášti. Jeho původ je vysvětlován jako důsledek smršťování hmoty v době diferenciace planetární hmoty, jako důsledek tření v souvislosti s projevy deskové tektoniky a v neposlední řadě rozpadem radioaktivních prvků a tepelnou energií uvolňovanou při skupenské přeměně roztavených hornin jádra na pevnou hmotu1. Geotermální energie je podle této definice spjata s endogenními (vnitřními) zdroji tepla.
Exogenním (vnějším) zdrojem tepla v horninovém prostředí je sluneční záření. Při dopadu slunečního záření na zemský povrch dochází k přeměně elektromagnetického záření na teplo. Základní informaci o distribuci sluneční energie mezi atmosféru a zemský povrch poskytuje např. Wikipedia12. Legislativa některých států považuje veškeré teplo pod zemským povrchem (bez ohledu na jeho původ) za geotermální energii2.
Pro rozlišení oblastí okupovaných výhradně geotermální energií a oblastí se smíšeným zastoupením energie (geotermální a dodané sluncem) lze použít následující schéma, převzaté z Rybach a Sanner (2000)2.
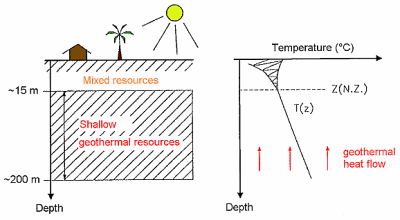
Obr. 2.1 Teplotní profil a zóny výskytu geotermální a sluneční energie
Teplota horninového prostředí směrem do podloží vzrůstá. Do určité hloubky pod zemským povrchem (oblast s rozkyvem teplot v pravé části obrázku 2.1) je teplota horninového masivu ovlivňována "aktuálními" klimatickými podmínkami - především denním a ročním cyklem teploty, infiltrací, výparem a dopadem slunečního záření. Řídícím činitelem pro vývoj teplot zemského povrchu a klimatu je přísun sluneční energie. Během světlé části dne (oproti nočnímu období) a v průběhu jara a léta (oproti podzimu a zimě) dochází k prohřívání horninového masivu od povrchu terénu do podloží.
Kontinuálním měřením teplot půdy v hloubkách 5 - 100 cm na území ČR se zabývají vybrané meteorolotické stanice ČHMÚ, například stanice v Doksanech3.
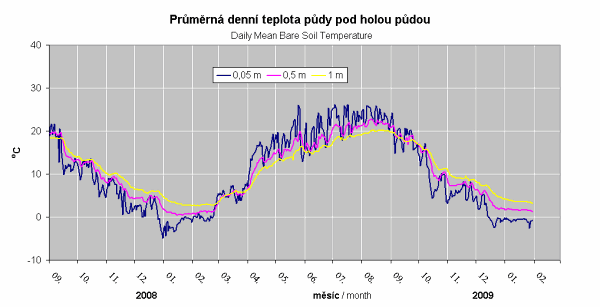
Obr. 2.2 Časové průběhy teplot s hloubkou
Z obr. 2.2 je patrné, že přibližně od září 2008 do března 2009 byla teplota při zemském povrchu nižší než teplota v hloubce 1 m. Naopak přibližně od května do srpna 2009 byla teplota při zemském povrchu větší. V tomto období docházelo k prohřívání hlubších partií horninového prostředí od prohřátého povrchu a tím i k transportu sluneční energie do horninového masivu. V hloubkách max. jednotek metrů pod povrchem terénu se v horninovém prostředí již neprojevuje denní amplituda chodu teplot na povrchu terénu. V hloubkách přibližně 15 m pod zemským povrchem je na území ČR teplota horninového masivu již obvykle konstantní a pouze nevýznamně převyšuje průměrnou roční teplotu povrchu terénu.
Hloubka cca 15 m je zároveň hranicí, pod kterou již tepelná energie dodaná Sluncem neproniká, neboť k šíření tepla může docházet pouze z oblastí s vyšší teplotou do oblastí s nižší teplotou. Masiv horniny v hloubkách větších než 15 m má za přirozených přírodních podmínek trvale vyšší teplotu než nadloží (viz obr. 2.1) - dochází k nárůstu teploty s hloubkou. Postulát o šíření tepla mezi oblastmi s rozdílnou teplotou bude v následujících kapitolách připomenut jako tzv. Fourierův zákon.
3 Bilance tepla
Matematický popis transportu tepla v horninovém prostředí je založen na zákonu zachování energie a zákonu zachování hmoty. Dříve místo pojmu teplo bylo užíváno termínu tepelná energie4. Teplo se obvykle označuje symbolem Q a jeho jednotkou je joule (J).
Množství tepla naakumulované v libovolné látce je určeno její teplotou. Vztah mezi teplotou a teplem definuje měrná tepelná kapacita c (J.kg-1K-1). Celkové množství tepla Q obsažené v jednotkovém množství látky přímo závisí na aktuální teplotě a na měrné tepelné kapacitě látky:
![]()
Rovnice je zjednodušená, platí pouze za předpokladu, že při ochlazování k absolutní nule nedochází k změnám skupenství a tepelná kapacita je v celém teplotním rozsahu konstantní.
Horninové prostředí se skládá z pórů a z pevné fáze. Póry mohou být vyplněny vodou, nebo vodou a vzduchem. Měrná tepelná kapacita jednotkového množství (1 kg) horninového prostředí bude záviset na pórovitosti n (-), mineralogickém složení pevné fáze a na stupni nasycení pórů vzduchem Sa (-) a na stupni nasycení pórů vodou Sw (-). Pro zvodněné horninové prostředí lze měrnou tepelnou kapacitu chorniny vyčíslit:
![]()
kdy cw, cs, a ca jsou měrné tepelné kapacity vody, pevné fáze a vzduchu. Stupeň nasycení vodou Sf, respektive vzduchem Sa je dán podílem objemu vody Vw a objemu pórů Vp, respektive podílem objemu vzduchu a pórů.
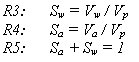
4 Rovnice transportu tepla
V horninovém prostředí zemské kůry se mohou uplatnit dva mechanismy přenosu tepelné energie:
- Unášení tepla vlivem proudění podzemní vody (tzv. konvektivní transport tepla),
- Přestup tepla horninovým prostředím z oblastí s větší tepelnou energií (teplotou) do oblastí s nižší tepelnou energií (tzv. konduktivní transport tepla).
Transport, respektive měrný tepelný tok označujeme symbolem qT. Jednotkou tepelného toku jsou (W.m-2), respektive (J.s-1.m-2), jeho velikost udává tzv. Fourierův zákon:
![]()
Velikost konduktivního tepelného toku je dána součinem koeficientu tepelné vodivosti horninového prostředí λ (W.m-1.K-1) a gradientu teploty grad (T) (K).

Tab. 4.1 Tepelné vodivosti vybraných látek14
Z tabelárních údajů tepelné vodivosti vybraných látek je zřejmé, proč mají nejlepší vlastnosti tepelně izolační materiály, které obsahují velké množství pórů vyplněných vzduchem, a proč průnik vody do tepelně izolačních materiálů jejich vlastnosti znehodnocuje.
Konvektivní transport tepla v horninovém prostředí vlivem proudění podzemní vody o dané teplotě závisí na hustotě vody ρ (kg.m-3), měrné tepelné kapacitě vody cw (J.kg-1K-1), její teplotě T (K) a na velikosti proudění popsané tzv. darcyovským tokem v (m.s-1).
![]()
Směr šíření tepla je v případě konvektivního transportu shodný se směrem proudění podzemní vody.
Citace:
1. Graeme Ross Beardsmore G. R., Cull J. P.; Crustal heat flow: a guide to measurement and modelling; 2001
2. Rybach L., Sanner B.; GROUND-SOURCE HEAT PUMP SYSTEMS - THE EUROPEAN EXPERIENCE; GHC BULLETIN, MARCH 2000
3. http://www.chmi.cz/meteo/ok/oba/obs/akt.html
4. http://cs.wikipedia.org/wiki/Teplo
5. http://water.usgs.gov/software/lists/groundwater/
6. Langevin, C.D., Thorne, D.T., Jr., Dausman, A.M., Sukop, M.C., and Guo, Weixing; SEAWAT Version 4: A Computer Program for Simulation of Multi-Species Solute and Heat Transport: U.S. Geological Survey; Techniques and Methods Book 6, Chapter A22, 39 p.; 2007
7. Langevin Ch. D., Langevin, C.D., Shoemaker W. B., Guo W.; MODFLOW-2000, the U.S. Geological Survey Modular Ground-Water Model Documentation of the SEAWAT 2000. Version with the Variable-Density Flow Process (VDF) and the Integrated MT3DMS Transport Process (IMT); U.S. GEOLOGICAL SURVEY - Open-File Report 03-426; 2003
8. Guo W.; Langevin Ch. D.; User's Guide to SEAWAT: A Computer Program For Simulation of Three-Dimensional Variable-Density Ground-Water Flow; U.S. Geological Survey; Techniques of Water-Resources Investigations 6-A7; 2002
9. http://www.feflow.info/
10. http://www.geophysik.rwth-aachen.de/html/shemat.php
11. odkaz k S_1D
12 http://en.wikipedia.org/wiki/Earth%27s_energy_budget
13. Langevin, C.D., Thorne, D.T., Jr., Dausman, A.M., Sukop, M.C., and Guo, Weixing, 2007, SEAWAT Version4: A Computer Program for Simulation of Multi-Species Solute and Heat Transport: U.S. Geological SurveyTechniques and Methods Book 6, Chapter A22, 39 p.
14. http://tepelna-vodivost.navajo.cz/
15. http://www.tzb-info.cz/3665-vrty-do-horninoveho-masivu-zdroj-energie-pro-tepelna-cerpadla-v
V dalších dílech: Modelování transportu tepla a přehled výsledků.
The discussion on the topic of the geothermal energy is carried out in the first part of the article. The basic equations relating convective and conductive heat transport to the groundwater flow and thermal heat conductivity are given. The heat storage is discussed as well.
The second and third part of the article describes simulation result for the vertical borehole for heat pump. The MODFLOW and MT3DMS software application is a bit curious, but the permissible simulation set up. Under the minimal or zero groundwater flow condition the vertical borehole heat pump predominately depletes geothermal energy accumulated in the rock. Dynamic heat resources, solar energy and earth geothermal heat flow, can not balance the heat pump extraction. The rock temperature declines all the working life of the heat pump. The temperature recovery after the heat pump termination is much longer compare to its working life. Globally the Earth geothermal heat resources are virtually inexhaustible. But locally in the vicinity of heat pumps heat resources could decline in such manner, that the heat pump operation will be uneconomical.