Vrt pro tepelné čerpadlo - model dlouhodobé energetické bilance - 2. část
Simulaci transportu tepla v horninovém prostředí v rámci "mělké geotermie" umožňuje provést řada komerčního i volně dostupného softwaru. V realizovaných simulacích byl transport tepla řešen na podkladě konceptu programu SEAWAT6,7,8.
5.1 Software
Simulace transportu tepla v horninovém prostředí umožňuje v současnosti řada komerčního i volně dostupného softwaru. Z volně dostupných programů lze na stránkách USGS5 najít například programy: HST3D, HYDROTHERM, SUTRA-MS, nebo SEAWAT. V realizovaných simulacích byl transport tepla řešen na podkladě konceptu programu SEAWAT6,7,8. Tento program v sobě kombinuje modifikovaný výpočetní kód programů MODFLOW a MT3DMS. Vzhledem k autorově dobré znalosti posledních dvou programů byly realizované simulace transportu tepla vypočteny pomocí těchto programů - nebyl využíván přímo program SEAWAT. Realizovaný výpočet teplotního pole v okolí tepelného čerpadla pomocí programů MODFLOW a MT3DMS je spjat se zjednodušujícími předpoklady, podrobněji popsanými v kapitole 5.4.
Mezi komerční software pro výpočet proměnlivě nasyceného proudění podzemní vody a transportu tepla patří například program FeFlow9. Část provedených kontrolních výpočtů byla realizována v programu SHEMAT10.
Český software, s možnostmi simulace duálního proměnlivě nasyceného proudění podzemní vody, transportu rozpuštěných látek a tepla, zaměřený na detailní popis procesů v nesaturované zóně, je program S1D. Program je vyvíjen při katedře hydrauliky a hydrologie na Českém vysokém učení technickém v Praze prof. Tomášem Vogelem.
5.2 Vstupní data matematického modelu transportu tepla
Konvektivní a konduktivní transport tepla v pórovém horninovém prostředí včetně lokálních zdrojů/odběrů tepla popisuje parciální diferenciální rovnice druhého řádu:
![]()
Pro zadání modelové simulace transportu tepla je nutné mít k dispozici následující okruhy informací (vstupních dat):
- prostorová interpretace darcyovského rychlostního pole proudění podzemní vody &nu (m.s-1),
- prostorová interpretace tepelné vodivosti zvodněného horninového prostředí &lambda (J.s-1.m-1. K-1),
- prostorová interpretace měrné tepelné kapacity vody a matrice horninového prostředí cw, respektive cs (J.kg-1.K-1),
- údaje objemové hmotnosti vody, respektive matrice horniny &rhow, respektive &rhos (kg.m-3),
- údaje o počátečním rozložení teplot v prostoru modelu T (K),
- prostorovou interpretaci pórovitosti n (-),
- údaje o zdrojích, nebo odběrech tepla H (J.s-1.m-3), vyjádřené pomocí objemové hustoty tepelného toku.
Uvedený výčet informací umožňuje vyčíslit všechny proměnné rovnice R8. V horninovém masivu bez proudění podzemní vody je konvektivní složka transportu tepla (&rhof.cf.T.&nu) nulová.
Proudění podzemní vody v horninovém masivu přerozděluje proudění tepla z oblastí infiltrace do oblastí drenáže. Při komplexním posuzování struktur s prouděním podzemní vody z hlediska potenciálu geotermální energie je pro výpočet transportu tepla nezbytná znalost rychlostního pole proudění podzemní vody. Informace je obvykle získána z modelové simulace proudění podzemní vody.
Tepelná vodivost &lambda a měrná tepelná kapacitu c jsou transportní charakteristiky matematického popisu proudění tepla. Tyto charakteristiky ovlivňují rychlost změn teploty horninového prostředí v důsledku změn směrů proudění podzemní vody nebo v důsledku odběrů tepla do tepelného výměníku tepelného čerpadla. Tepelná vodivost se mění v závislosti na mineralogickém složení horniny, pórovitosti a v závislosti na stupni nasycení horninového masivu vodou.
Zadáním počátečního rozložení teplot horninového masivu (počáteční podmínky) je definována počáteční energetická bilance prostoru modelu.
Geotermální energie (teplo) proudí vlivem kondukce k zemskému povrchu. Pro simulace vlivu tepelných čerpadel je nutné znát informaci o velikosti zemského tepelném toku qzemě. Tepelný tok Země je v modelech transportu tepla zadáván ve dně modelovaného prostoru, ve formě okrajové podmínky.
5.3 Metodika simulace tepelného čerpadla
V modelové simulaci jsme se zaměřili na popis proudění tepla v okolí tepelného čerpadla země/voda s tepelným výměníkem (výparníkem) situovaným ve vertikálním vrtu.
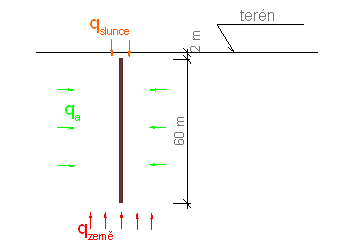
Obr. 5.1 Proudění tepla v okolí tepelného čerpadla
Spuštění provozu tepelného čerpadla způsobí v horninovém prostředí proudění tepla směrem ke stvolu vrtu s tepelným výměníkem. Zdrojem tepla pro tepelné čerpadlo se stane:
- geotermální tok země qzemě (na našem území v rozmezí 30 - 110 mW.m-2),
- teplo naakumulované v horninovém masivu před zahájením činnosti tepelného čerpadla qa,
- teplo přijaté z energie slunce přes zemský povrch qslunce,
- konvektivní tepelný tok způsobený prouděním podzemní vody qkonvekce.
Realizované simulace vývoje teplotního pole v okolí tepelného čerpadla jsou po domluvě se zadavatelem provedeny při zanedbání vlivu proudění podzemní vody. Modelové zadání tak odpovídá umístění tepelného čerpadla např. v oblasti masivu granitu v blízkosti rozvodnice (tzn. zanedbatelné proudění) a při úrovni hladiny podzemní vody situované mělko pod povrchem terénu. Pro výpočet je zjednodušeně celý profil uvažován jako nasycený.
Proudění tepla v okolí tepelného čerpadla je popsáno pomocí následujících třech variant simulací:
- varianta transportu tepla bez tepelného čerpadla; v simulaci jsou popsány podmínky lokality před zahájením provozu tepelného čerpadla simulace je rovněž využita jako srovnávací pro analýzu změn tepla v horninovém prostředí namodelovaných v následujících variantách,
- varianta transportu tepla v okolí tepelného čerpadla při simulaci odběru tepla pomocí okrajové podmínky prvního typu
- varianta transportu tepla v okolí tepelného čerpadla při simulaci odběru tepla pomocí okrajové podmínky druhého typu
Realizované simulace vývoje teplotního pole v okolí tepelného čerpadla jsou po domluvě se zadavatelem provedeny při zanedbání vlivu proudění podzemní vody.
Proudění tepla v okolí tepelného čerpadla je popsáno pomocí následujících třech variant simulací:
- A. varianta transportu tepla bez tepelného čerpadla; v simulaci jsou popsány podmínky lokality před zahájením provozu tepelného čerpadla; simulace je rovněž využita jako srovnávací pro analýzu změn tepla v horninovém prostředí namodelovaných v následujících variantách,
- B. varianta transportu tepla v okolí tepelného čerpadla při simulaci odběru tepla pomocí okrajové podmínky prvního typu (Dirichletovy okrajové podmínky),
- C. varianta transportu tepla v okolí tepelného čerpadla při simulaci odběru tepla pomocí okrajové podmínky druhého typu (Neumannovy okrajové podmínky).
5.4 Vstupní předpoklady simulace - zjednodušení
Komplexní matematický popis proudění tepla, obsažený v programu SEAWAT413, umožňuje v simulaci zohlednit vliv teploty:
- na viskozitu vody a tím i vliv teploty na velikost proudění,
- na objemovou hmotnost vody a změny proudění v důsledku rozdílných hustot vody (tzv. density dependent flow).
V realizovaných simulacích variant A – C je vliv proudění podzemní vody na transport tepla v okolí tepelného výměníku čerpadla zanedbán - v simulacích není uvažováno proudění podzemní vody. Druhým zjednodušujícím předpokladem realizovaných výpočtů je uvažovaná rovnováha mezi teplotou matrice horninového masivu a podzemní vodou.
Při zavedení výše uvedených schematizací je možné výpočet teplotního pole řešit nezávisle na výpočtu proudění podzemní vody - a lze ho realizovat pomocí programů MODFLOW a MT3DMS. Pro matematický popis transportu tepla pomocí programu MT3DMS je využita tzv. advekčně-disperzní rovnice s lineární sorpcí kontaminantu na pevnou fázi horninového prostředí. Využití rovnice se sorpcí umožňuje simulovat výměnu tepla mezi matricí horninového prostředí a podzemní vodou. Zadání transportních parametrů vedení tepla do programu MT3DMS obsahuje manuál programu SEAWAT413.
5.5 Geometrie modelového prostoru, diskretizace
Povrch modelu má nadmořskou výšku 400 m n. m. Báze (dno) modelu je v úrovni 100 m pod terénem. Jeho nadmořská výška je 300 m n. m. Ve vertikálním směru je prostor modelu rovnoměrně diskretizován (rozdělen) pomocí 100 vrstev o mocnosti 1 m.
V horizontální rovině má modelový prostor tvar čtverce s délkou hrany 2000 m. Velikost modelových buněk je nerovnoměrná se zahuštěním v okolí tepelného čerpadla. Tepelné čerpadlo se nachází uprostřed modelu. Modelový výpočet transportu tepla je realizován na třírozměrné výpočetní síti.
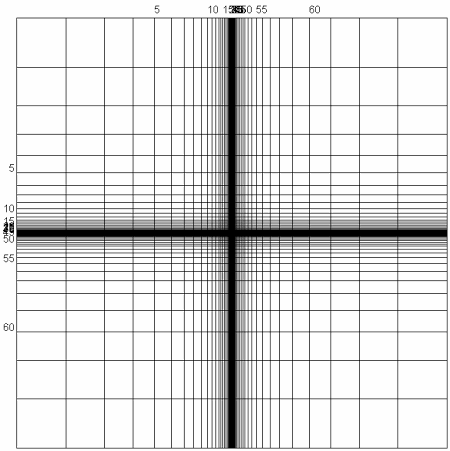
Obr. 5.2 Schéma výpočetní sítě
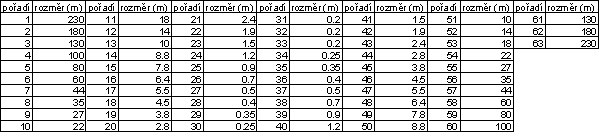
Tab. 5.1 Pořadí a rozměr hrany elementů výpočetní sítě
Hustota výpočetní sítě vzrůstá od okrajů ke středu. Tepelné čerpadlo je simulováno v buňce s pořadím 32 (32. řádek a 32. sloupec). Rohové buňky modelu mají rozměr 230.230 m. Buňka s tepelným čerpadlem má rozměr 0,2.0,2 m a přibližně odpovídá svojí plochou a průměrem instalovaným tepelným výměníkům ve vrtech. Elementy výpočetní sítě mají ve směru osy X a Y shodný rozměr.
5.6 Transporní charakteristiky výpočtu tepla
Modelová tepelná vodivost &lambda a měrná tepelná kapacita c je v celém prostoru modelu shodná. Zadané hodnoty transportních parametrů udává tabulka 2:

Tab. 5.2 Transportní charakteristiky zadané v realizovaných simulacích
Tepelná vodivost zvodněného horninového prostředí je vyčíslena jako vážený součet (podle pórovitosti) vodivosti horninové matrice a vody.
5.7 Okrajové podmínky simulace transportu tepla
Okrajová podmínka je zadána ve třech oblastech modelu:
- na bázi modelu (100. vrstva),
- při povrchu terénu (1. modelová vrstva),
- v prostoru tepelného čerpadla (3. - 62. centrální modelová buňka).
Bazální okrajová podmínka v prostoru modelu nahrazuje tepelný tok Země. Pro výpočet je bazální tepelný tok zadán hodnotou 60 mW.m-2 - ve středu reálného , udávaného rozpětí hodnot tepelného toku na území ČR. V modelu je zemský tepelný tok zadán pomocí zdroje tepla v každé modelové buňce a v celé délce simulací.
Zadaná okrajová podmínka prvního typu při povrchu terénu (konstantní teplota 8.5°C po celou dobu simulací) umožňuje simulovat odvod tepla z horninového prostoru - v přírodních podmínkách dochází k odvodu tepla přes rozhraní země/atmosféra. V oblasti tepelného čerpadla v důsledku snížení teplot naopak dochází k přísunu tepla z povrchu terénu ke stvolu vrtu.
Je známo, že na území ČR je v hloubce 10 - 20 m pod terénem teplota horninového masivu konstantní, odpovídající průměrné roční teplotě. Posunem modelované hranice konstantní teploty směrem k terénu dochází v realizovaných simulacích k určitému zjednodušení. Z obrázku 2.1 je patrné, že zafixováním teploty v první modelové vrstvě na hodnotě 8,5°C je tepelná bilance prostoru modelu zvýšena. (teploty mělko pod zemským povrchem jsou v období chodu tepelného čerpadla nižší než 8,5°C).
Odběr tepla horninovému masivu lze simulovat dvěma způsoby:
- zadáním okrajové podmínky prvního typu - teplota modelových buněk v prostoru tepelného výměníku je zafixována na hodnotě odpovídající průměrné teplotě technologie tepelného výměníku v období chodu tepelného čerpadla; nevýhodou tohoto přístupu je "nekontrolovaný" odběr tepla z horninového masivu, přesnost simulace bude záviset na správném nastavení teploty modelových buněk stvolu tepelného čerpadla; takovéto zadání modelu je zrealizováno ve variantě simulace "B"; v simulaci je teplota modelových buněk tepelného čerpadla zadána 2°C,
- zadáním okrajové podmínky druhého typu - celkové množství tepla odebrané tepelným výměníkem horninovému masivu je rozpočteno do jednotlivých modelových buněk simulujících výměník tepelného čerpadla - v simulaci je v obdobích chodu tepelného čerpadla zadán celkový odběr tepla 5kW; takovéto zadání modelu je zrealizováno ve variantě simulace "C"; i toto modelové zadání obsahuje určité nepřesnosti, protože skutečné množství odebíraného tepla se mění v čase a v prostoru; spodní okraj tepelného čerpadla odebere větší množství tepla než jeho centrální část.
Tepelné čerpadlo je zadáno v buňkách na řádku a sloupci 32. Ve vertikálním směru tepelné čerpadlo zaujímá 3. - 62. modelovou vrstvu. Délka stvolu tepelného čerpadla je 60 m (2 - 62 m pod terénem).
5.8 Délka simulace - výpočetní periody
Modelové simulace sestávají ze 100 výpočetních úseků (period):
- 1. perioda s délkou 100 dnů je určena k ustálení teplotního pole (odstranění nepřesností vázaných na načtení počáteční podmínky teplot horninového masivu pro podmínky přirozeného gradientu teploty s bazálním tokem tepla 60 mW.m-2),
- 2. - 99. perioda (střídání období klidu a chodu tepelného čerpadla v délce 183 a 182 dnů); délka 2. - 99. periody je 49 let a simulováno je období od 1.4.2010 do 1.4.2059; chod tepelného čerpadla je zadán ve 3. 5. 7. .... 97. a 99. periodě,
- 100. perioda - v délce 50 let je simulováno ustalování teplot po ukončení chodu tepelného čerpadla; (trvání 100. periody je od 1.4.2059 - 1.4.2109),
5.9 Počáteční podmínka simulací vlivu tepelného čerpadla
Teplota horninového prostředí s hloubkou vzrůstá. V rámci zvolené metodiky modelové simulace je počátek provozu tepelného čerpadla zadán z podmínek ustáleného vertikálního gradientu teploty zvodněného horninového masivu (obdobně jak je tomu v terénu). Tento přístup zajišťuje, že namodelované změny teplot horninového masivu po spuštění tepelného čerpadla souvisí výhradně s jeho činností.
Hodnoty počáteční podmínky pro simulace tepelného čerpadla byly stanoveny v samostatné pomocné simulaci, jejímž cílem bylo nastolení ustáleného proudění tepla od modelové báze směrem k terénu. Jako počáteční podmínka této pomocné simulace byla zadána v celém prostoru modelu konstantní teplota 8.5°C.
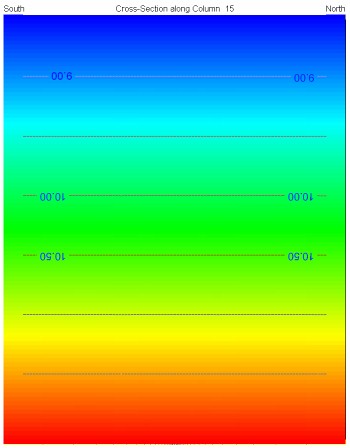
Obr. 5.3 Teploty počáteční podmínky simulací (varianty A, B, C)
Práce s modelem tepla (ve srovnání s modelováním proudění podzemní vody, nebo transportu rozpuštěných látek) vyžaduje nové postupy volby okrajových podmínek a zadání jiných hodnot transportních charakteristik (teplná vodivost, měrná tepelná kapacita).
Do popředí se dostává otázka ověření správnosti výsledků modelových simulací. Ověření věrohodnosti modelu lze provést jak kontrolou hodnot vstupních parametrů, tak kontrolou bilance modelové simulace. Pro ověření správnosti vypočteného teplotního pole v tomto jednoduchém případě lze použít Fourierův zákon (viz R6). Gradient teploty je dán podílem rozdílu teploty mezi 1. a 100. modelovou vrstvou (12.07 a 8.5 °C) a vzdálenosti těchto buněk (99 m):
gradT = (12.07 - 8.5)/99 = 0.036060 °C/m
Tepelný tok je dán součinem tepelné vodivosti zvodněného horninového prostředí a gradientu teploty.
qT = -λgrad(T) = 1.6625*0.036060 = 0.06W = 60 mW.m-2
Výsledné modelové rozložení teplot (viz obr. 5.3) je v souladu s Fourierovým zákonem a tepelný tok vypočtený z gradientu teploty a modelové tepelné vodivosti horninového masivu odpovídá simulovanému tepelnému toku Země (60 mW.m-2). Ke shodnému výsledku rozložení teplot v horninovém masivu vede i simulace proudění tepla v programu SHEMAT.
The discussion on the topic of the geothermal energy is carried out in the first part of the article. The basic equations relating convective and conductive heat transport to the groundwater flow and thermal heat conductivity are given. The heat storage is discussed as well.
The second and third part of the article describes simulation result for the vertical borehole for heat pump. The MODFLOW and MT3DMS software application is a bit curious, but the permissible simulation set up. Under the minimal or zero groundwater flow condition the vertical borehole heat pump predominately depletes geothermal energy accumulated in the rock. Dynamic heat resources, solar energy and earth geothermal heat flow, can not balance the heat pump extraction. The rock temperature declines all the working life of the heat pump. The temperature recovery after the heat pump termination is much longer compare to its working life. Globally the Earth geothermal heat resources are virtually inexhaustible. But locally in the vicinity of heat pumps heat resources could decline in such manner, that the heat pump operation will be uneconomical.