Nejnavštěvovanější odborný web
pro stavebnictví a technická zařízení budov

Vysokoteplotní akumulátor tepla s geopolymerem

Tepelně vodivý geopolymer a jeho aplikace v tepelném úložišti

30.6.2014

Ing. Matěj Černý, Fakulta životního prostředí, Česká zemědělská univerzita v Praze; PROGEO, s.r.o.

Recenzovaný

Přebytky energie je možné skladovat ve formě zjevného tepla. Prezentovaný koncept využívá horninový materiál a tepelně vodivý geopolymer ke konstrukci tepelného úložiště pracujícího s teplotami do 400 °C. Článek popisuje modelové vyhodnocení vlivu vybraných materiálů úložiště.

Úvod

Při hrozbě globální klimatické změny a znečištěného životního prostředí, je hospodaření s energií velmi diskutovaným tématem. V energetickém průmyslu jsou hlavní trendy zaměřeny na obnovitelné zdroje a úspory energie [22]. Nevýhodou energie pocházející z obnovitelných zdrojů, primárně větrné a sluneční, je časový nesoulad mezi její nabídkou (výrobou) a poptávkou. Tento problém může být kompenzován užitím tepelných úložišť [7, 8]. Úspory energie může být rovněž dosaženo uložením a následným využitím odpadního tepla z průmyslových procesů [9, 12].

Jedna z klasifikací tepelných úložišť je na základě jejich provozní teploty. Nízkoteplotní tepelná úložiště využívána k vytápění a klimatizaci budov [3, 9] pracují pod 120 °C, [7], resp. 200 °C [5]. Vysokoteplotní tepelné úložiště energie obvykle pracují při teplotách nad 350 °C. Jejich nejčastější nasazení je v solárních tepelných elektrárnách, ve kterých je sluneční energie za pomoci vysokoteplotní páry a turbín transformována na elektrickou energii [7]. Tepelné úložiště umožňuje produkci v tomto typu solárních elektráren i za zvýšené oblačnosti či po setmění.

Existují tři základní principy způsobu ukládání tepla. První typ používá zjevné (citelné) teplo. Uložená energie je úměrná rozdílu teplot a tepelné kapacitě dané látky. Pokud je k akumulaci využívána změna skupenství, energie je ukládána ve formě latentního tepla, což je druhý princip [13]. Třetí tzv. termo-chemické skladování využívá endotermické a exotermické reverzibilní chemické reakce [5]. První dva typy jsou častější, třetí je stále vyvíjen [1, 4].

Materiál tepelného úložiště využívající zjevného tepla z pevné fáze nepodléhá fázové přeměně v teplotním rozsahu procesu skladování. Schopnost ukládat zjevné teplo pro daný materiál je dána tepelnou kapacitou na jednotku objemu. Aby byl materiál vhodný pro tepelné úložiště, musí být levný a mít dobrou tepelnou vodivost [6]. Přenos tepla do nebo z transportní teplonosné tekutiny zajišťuje tepelný výměník. V případě nižší tepelné vodivosti materiálu úložiště, rostou vstupní náklady na geometricky komplikovanější tepelný výměník. V literatuře je uvedeno testování lité keramiky nebo specificky navrženého betonu ve španělské solární elektrárně Plataforma Solar de Almería pod vedením Německého střediska pro letectví a kosmonautiku (Deutsches Zentrum für Luft- und Raumfahrt e. V. – dále jen DLR) [12, 19, 20]. Jako další levný kandidát byla studována recyklovaná průmyslová keramika vyrobená vitrifikací odpadů obsahujících asbest [14, 15].

Hlavní idea výzkumného projektu Reverzibilní skladování energie (RESEN) [17], je založena na využití hornin pro akumulaci tepla a materiálu zlepšujícího tepelnou vodivost úložiště. Pro lepší rozvod tepla v úložišti byl vyvinut tepelně vodivý geopolymer (TVG) [21].

Článek dokumentuje modelové porovnání termodynamického chování úložiště při užití různých materiálů včetně TVG. Porovnání je provedeno na základě numerického modelu tepelného transportu v úložišti programem COMSOL Multiphysics [2], který byl například využit pro modelování zahřívání horninového masivu [16] nebo ke studiu geotermálního systému [18].

Reverzibilní skladování energie

Na počátku projektu RESEN byla provedena analýza běžných hornin z území České republiky. Na vzorcích ze 41 lokalit byly změřeny geomechanické vlastnosti. Byly vybrány 4 sedimentární horniny, 12 vulkanitů, 9 plutonitů a 16 metamorfovaných hornin. Pro srovnání byl testován i vzorek běžného betonu. Deset vhodných kandidátů bylo vybráno k širšímu zkoumání a k analýze tepelných vlastností. Optimální horninou pro tepelná úložiště byl vyhodnocen granit z lokality Panské Dubenky. Tento granit vykazuje nejvyšší tepelnou kapacitu a nejnižší pokles tepelné vodivosti s rostoucí teplotou. Zároveň byla prokázána jeho stabilita při opakované tepelné zátěži při teplotách 400 °C.

S cílem zlepšení tepelné vodivosti materiálu tepelného úložiště byl vyvíjen vysoce tepelně vodivý materiál založený na směsi geopolymeru s grafitem. Přesněji směsi vodního skla, metakaolinu a vločkového grafitu různých velikostí. Materiál je tepelně odolný a má 6 až 10× vyšší vodivost oproti běžným horninám. Cyklický ohřev TVG prokázal stabilitu do 400 °C za přítomnosti atmosférického kyslíku. Tepelná stabilita základního geopolymeru je více než 800 °C, ale maximální pracovní teplota je limitována vodivými aditivy, které jsou oxidovány při teplotách nad 400 °C. Tepelná vodivost a kapacita vzorků užívaných materiálů byla změřena přístrojem Hot Disk Thermal Constants Analyser. Výsledné hodnoty jsou 19,7–23,3 W∙m⁻¹K⁻¹ a 1,05–1,51 MJ∙m⁻³K⁻¹ v závislosti na rozložení zrnitostních frakcí užitých aditiv. Ostatní parametry tepelně vodivé hmoty jsou: objemová hmotnost 1150 kg∙m⁻³; pórovitost 40 %; pevnost v prostém tlaku 4 MPa.

Projektované teplené úložiště využívající kombinaci granitových kostek a tepelně vodivého geopolymeru (v grafech označeno granit + TVG) bylo porovnáno s objemově totožným úložištěm využívající betonový nebo granitový monoblok. V simulacích byly zadány dva druhy betonů, jeden „běžný“, popsaný Gil a kol. [7] a druhý „vysokoteplotní“ vyvinutý v DLR pro aplikaci v tepelných úložištích s vysokou tepelnou kapacitou [10].

Prototyp tepelného úložiště

Na Obr. 1 je schematicky znázorněna geometrie zrealizovaného prototypu úložiště. Červeně je akumulační jádro sestávající z granitových kostek spojených TVG. Strana krychlového akumulačního jádra je 800 mm dlouhá, strany granitových kostek mají rozměr 90 mm. Rozevření spár vyplněných TVG je 10 mm. V modelové variantě s granitovým (nebo betonovým) monoblokem je geometrie kostek nahrazena jednou krychlí o stejném objemu. Menší kvádr pod jádrem vymezuje tepelnou izolaci FoamGlas (podlahový), kvádr kolem celého úložiště vymezuje rozsah minerální izolace Loose Wool s mocností 300 mm.

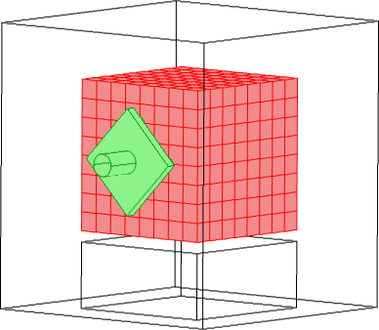
Obr. 1a Geometrie tepelného úložiště. Betonový/granitový monoblok zaujímá stejný objem jako granitové kostky s TVG. Jádro červeně, soustava tepelného výměníku zeleně.

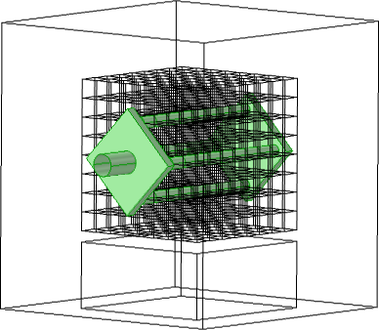Obr. 1b Geometrie tepelného úložiště. Betonový/granitový monoblok zaujímá stejný objem jako granitové kostky s TVG. Jádro červeně, soustava tepelného výměníku zeleně.

Obr. 1 Geometrie tepelného úložiště. Betonový/granitový monoblok zaujímá stejný objem jako granitové kostky s TVG. Jádro červeně, soustava tepelného výměníku zeleně.

Zdroj tepla v prototypu úložiště je realizována elektrickými topnými odporovými tyčemi, sledováno je množství dodané energie. Jedna topná tyč je umístěna ve středu krychle a čtyři na úhlopříčkách akumulačního jádra souběžně s trubicemi tepelného výměníku, vždy 20 cm od stěny akumulačního jádra. Topné tyče mají délku 40 cm s průměrem 1,2 cm. Nominální výkon jedné tyče je 900 W, což odpovídá maximálnímu příkonu 4500 W pro celé úložiště. Jednotlivé topné tyče byly spínány termoregulačními členy dle požadované teploty na jejich povrchu.

Odběr tepla z prototypu je uskutečňován proudícím vzduchem uvnitř tepelného výměníku (na Obr. 1 zeleně). Vzduch je nasáván z laboratoře ventilátorem. Trubicí o průměru 125 mm je veden do rozdělovacího prvku, ze kterého jsou vyústěny 4 tenkostěnné trubice vedoucí skrz akumulační jádro. Průměr trubic je 60 mm. Za vyústěním z akumulačního jádra je umístěn slučovací prvek tvarově identický s rozdělovacím prvkem. Před vstupem do rozdělovacího prvku je umístěn zchlazovací anemometr s teplotním čidlem. Na výstupu ze slučovacího prvku je umístěna Prandtlova trubice a teplotní čidlo. Vstupní rychlost proudění byla udržována konstantně na úrovni 4,5 m∙s⁻¹.

Numerický model

Numerický model byl zpracován v programu COMSOL Multiphysics [2], který využívá metody konečných prvků. V modelu byl simulován pouze konduktivní přenos tepla. Z původního záměru simulovat turbulentní proudění vzduchu uvnitř tepelného výměníku bylo upuštěno, z důvodů vysoké výpočetní náročnosti spárovaného výpočtu Navier-Stokesových rovnic s konvektivním transportem tepla.

Zdroj tepla byl simulován okrajovou podmínkou prvního typu na plášti topných tyčí, tj. byla zadána hodnota teploty. Odběr tepla byl simulován okrajovou podmínkou reprezentující konvektivní ochlazování (resp. Newtonův ochlazovací zákon) s koeficientem přestupu tepla odpovídajícímu nucenému proudění v trubicích s průměrem 60 mm a měřené rychlosti proudění uvnitř výměníku (h = 25,4 W∙m⁻²K⁻¹). Tepelné ztráty pláštěm modelového úložiště byly simulovány okrajovou podmínkou konvektivního ochlazování s přirozeným prouděním na vertikální stěně (h = 3,4 W∙m⁻²K⁻¹). Okolní teplota v laboratoři byla zadána konstantní po celou dobu experimentu T = 18 °C.

V Tab. 1 jsou uvedeny hodnoty materiálových parametrů zadaných do modelu. Pro granit z Panských Dubenek (označen: granit PD) a TVG byl použit funkční vztah hodnot parametrů a teploty.

Tab. 1 Parametry simulovaných materiálů při teplotě 20 °C
hodnoty při 20 °C	součinitel tepelné vodivosti `λ` [W∙m⁻¹K⁻¹]	měrná tepelná kapacita `Cp` [J∙kg⁻¹K⁻¹]	hustota `ρ` [kg∙m⁻³]
beton	1,5	850	2200
beton (DLR)	1	916	2750
granit PD	2,55	793	2620
TVG	21,5	913	1150

Porovnání tepelné bilance úložiště pro 4 varianty materiálového řešení je zpracováno pro dva scénáře:

Jednorázové nabíjení a vybíjení po dobu 200 hodin.
Cyklický režim nabíjení a vybíjení s délkou cyklu 24 hodin.

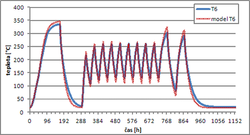
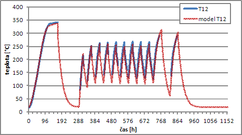
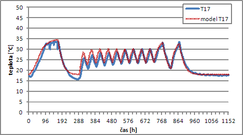
Kalibrace modelu termodynamického chování tepelného úložiště proběhla pro data naměřená pro realizovanou variantu konglomerátu granitových kostek a TVG. Experimentální výsledky jsou v dostatečné shodě s modelovou předpovědí. Průběh simulovaných a měřených hodnot z vybraných čidel je vynesen v grafu na Obr. 2. Na realizaci prototypu úložiště bylo použito 0,37 m³ žuly z lokality Panské Dubenky a 0,14 m³ tepelně vodivého geopolymeru.

Ukázka docílené shody modelových a měřených teplot na vybraných teplotních čidlech je na grafech z Obr. 2. Čidlo T6 je umístěno poblíž centrální topné tyče, čidlo T12 je u trubice výměníku a čidlo T17 reprezentuje povrchové teploty opláštění úložiště. Rozdíly mezi měřením a simulací jsou pravděpodobně způsobeny především idealizovanou modelovou geometrií úložiště (v modelu mají všechny granitové kostky identický rozměr a tepelné vlastnosti, což je v rozporu s heterogenitou přírodních materiálů a vzniklými nepřesnostmi při opracování; v modelu je také zadáno identické rozevření tepelně vodivých spár a jejich homogenní tepelné charakteristiky v celém objemu úložiště.

Obr. 2a Porovnání měřených a modelových teplot na vybraných čidlech

Obr. 2b Porovnání měřených a modelových teplot na vybraných čidlech

Obr. 2c Porovnání měřených a modelových teplot na vybraných čidlech

Obr. 2 Porovnání měřených a modelových teplot na vybraných čidlech

Jednorázové nabití

Ve scénáři ohřevu úložiště 200 hodin bylo simulováno maximální nabití úložiště. Z vyneseného průběhu hodnot uloženého tepla (viz Obr. 3) s využitím různých materiálů je patrné, že užití TVG v kombinaci s granitem umožňuje nejrychlejší nabíjení úložiště.

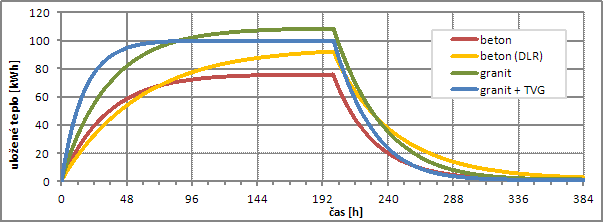
Obr. 3 Průběh hodnot uloženého tepla při 200hodinovém cyklu

Po cca 84 hodinách dochází k protnutí křivek naakumulovaného tepla v granitovém monobloku a konglomerátu TVG s kostkami. Po tomto časovém okamžiku je v konglomerátu uloženo méně tepla. Příčina spočívá v poněkud menší schopnosti akumulace tepla v jednotkovém objemu TVG ve srovnání s jednotkovým objemem granitu z důvodu nižší objemové tepelné kapacity TVG., Toto menší absolutní nabití konglomerátu je vyváženo podstatně zvýšenou dynamikou úložiště.

Obr. 4a Fotografie německého (DLR) testovacího tepelného úložiště ve španělské Plataforma Solar de Almería [10, 11]

Obr. 4b Fotografie německého (DLR) testovacího tepelného úložiště ve španělské Plataforma Solar de Almería [10, 11]

Obr. 4 Fotografie německého (DLR) testovacího tepelného úložiště ve španělské Plataforma Solar de Almería [10, 11]

Z průběhu hodnot uloženého tepla ve vysokoteplotním betonu (DLR) je patrné, že ani po 200 hodinách nabíjení nedošlo k ustálení a dosažení maximální úložné kapacity. Nejpomalejší nabíjení je dáno jeho nejnižší tepelnou vodivostí. Opodstatnění využití tohoto typu betonu je při dlouhých dobách nabíjení a odběru, nebo, jak je i patrno z fotografií prototypu německého úložiště (Obr. 4) – při velmi hustém registru trubic tepelného výměníku.

Cyklický režim 12/12 h

Scénář s 24 hodinovým cyklem sestává z 12 hodin nabíjení a 12 hodin odběru. Ve všech variantách je zapotřebí 4 až 5 cyklů k ustálení pracovních teplot a uloženého množství tepla (viz graf na Obr. 5).

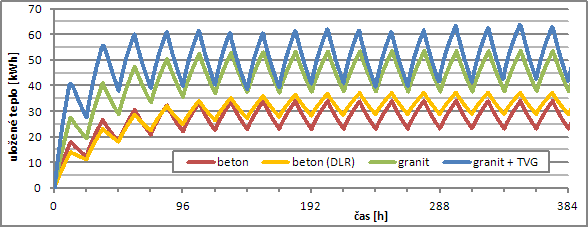
Obr. 5 Graf simulovaných průběhů uloženého tepla v tepelném úložišti, granitovém a betonovém monobloku

Z pohledu hodnocení nejsou tolik důležité absolutní hodnoty, ale rozdíl mezi maximálním a minimálním nabitím. Tato hodnota udává množství využitelného tepla při popsaném pracovním cyklu.

Pro granitový monoblok se ustálené hodnoty uloženého tepla pohybují mezi hodnotami 37,7 (při vybití) a 53,7 kWh (po nabití). Rozdíl činní 16 kWh využitelného tepla. Simulované hodnoty pro betonový monoblok se po ustálení pohybují mezi minimem 23 kWh a maximem 34,2 kWh (rozdíl 11,1 kWh uloženého tepla). Při simulaci vysokoteplotního betonu (DLR) byla získána nejmenší amplituda využitelného tepla 8,5 kWh). Pro úložiště sestavené z granitových kostek a TVG se akumulované teplo pohybuje v intervalu 41,5–63,7 kWh (využitelné akumulované teplo 22,2 kWh). Dle modelu, tak umělé úložiště s TVG umožňuje v rámci pracovního cyklu 12/12 hod uložit o 31 % více tepla oproti granitovému monobloku.

Provedené výpočty dokládají vhodnou volbu zvoleného výplňového materiálu úložiště i přínos TVG. V grafu na Obr. 6 jsou vyneseny minimální a maximální teploty jádra úložiště.

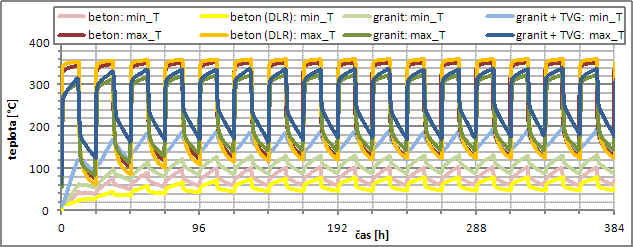
Obr. 6 Graf průběhů simulovaných minimálních (min_T) a maximálních (max_T) teplot v jádru (viz Obr. 1) úložiště z monobloků nebo granitových kostek s TVG)

Větší rozdíly minimální a maximální teploty úložiště dokumentují jeho větší tepelné namáhání. Minimální teploty granitového monobloku (na Obr. 5 světle zeleně) v ustáleném režimu plnění a prázdnění teplem kolísají v rozmezí 85 až 135 °C. Minimální teploty jádra z kostek a TVG (na Obr. 5 světle modře) kolísá v ustáleném režimu v rozmezí 125 až 170 °C. Velikost rozkyvu minimálních teplot je pro obě varianty podobná (45–50 °C). Maximální teploty granitového monobloku (na Obr. 5 modře) se v ustáleném režimu plnění a prázdnění kolísají v rozmezí 140 až 320 °C, teploty kostek s TVG byly simulovány v rozmezí 170 a 300 °C (na Obr. 5 zeleně). Tyto výsledky dokumentují, že v simulovaných scénářích způsobuje přítomný TVG lepší distribuci tepla (méně výrazné extrémy) a vyšší průměrnou provozní teplotu. Nejvyšší amplitudu maximálních teplot vykazuje vysokoteplotní betonový monoblok (123–360 °C), minimální teploty se pohybují mezi 47 a 81 °C. Maximální teploty v monobloku z obyčejného betonu byly simulovány v rozmezí 130–350 °C, minimální teploty se pohybují mezi 55 a 100 °C.

Na Obr. 7 jsou vlevo vyneseny průměrné teploty jádra úložiště, které téměř kopírují množství uloženého tepla. Vpravo na stejném obrázku je graf znázorňující rozdíl maximální a minimální teploty jádra. Ve fázi vybití je v jádru z kostek a TVG maximální rozdíl teplot cca 40 °C, v granitovém monobloku je to o 10 °C více. Výraznější rozdíl je po nabití, kdy maximální rozdíly uvnitř granitového monobloku dosahují hodnoty přes 200 °C, v obyčejném betonu 270 °C a v jádru z vysokoteplotního betonu až 300 °C. Pro jádro s TVG rozdíl minimální a maximální teploty vychází pod 140 °C.

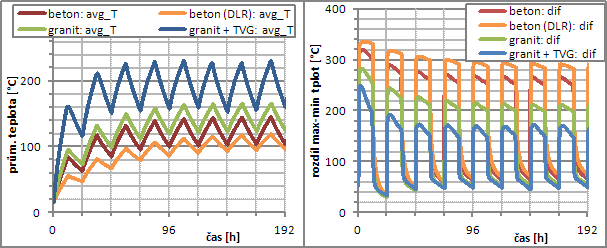
Obr. 7 Vlevo průběh průměrné teploty jádra; vpravo průběh rozdílu maximální a minimální teploty jádra v daném okamžiku při 12h cyklickém provozu

Simulace byly sestaveny tak, aby dlouhodobě nebyl překročen příkon topných tyčí 4,5 kW a zároveň aby lokálně nebyla překročena teplota 400 °C. Z provedených výpočtů vyplývá, že teplota úložiště při cyklu trvajícím 12 hod nedosáhne projektovanou maximální teplotu 400 °C. Východiskem je prodloužení cyklu nabíjení a vybíjení úložiště. Z tohoto důvodu byla zpracována simulace pro 48hodinový cyklus. Trendy výsledků jsou obdobné, proto zhodnocení je pouze ve formě následující tabulky se slovním komentářem.

V Tab. 2 jsou uvedeny simulované hodnoty využitelného tepla a procentuálně porovnány s variantou granitového monobloku.

Tab. 2 Shrnutí výsledků tří scénářů nabíjení (jednorázové, cyklické 12/12h a cyklické 24/24h)
a čtyř variant použitých materiálů úložiště

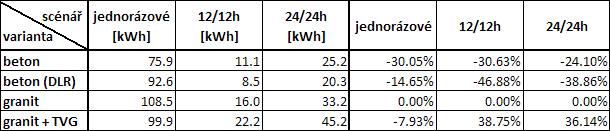
Při cyklickém režimu využití úložiště je nejefektivnější použití TVG v kombinaci s granitem. Při porovnání variant 12/12 hod a 24/24 hod byl stanoven přínos TVG na 36–39 % pro množství využitelného tepla. Použití betonu snižuje kapacitu identického úložiště o 24–30 % podle uvažované délky cyklu. Vysokoteplotní beton (DLR) se pro navrhované uspořádání úložiště jeví nevhodně.

Vyústěním modelového návrhu úpravy designu úložiště s cílem zmenšit pokles teploty vzduchu z tepelného výměníku bylo liniové uspořádání.

Liniové uspořádání

Pro účely komerčního užití je možné prototyp tepelného úložiště modifikovat s cílem zajistit optimální provoz. Základním parametrem modifikace je změna rozměrů. Touto změnou lze docílit řádově větší kapacitu úložiště a podstatně tak lze modifikovat i teplotu na výstupu z tepelného výměníku.

Udržení vyšších teplot vystupujícího vzduchu z tepelného výměníku po delší časové období lze nejsnáze docílit při liniové geometrii úložiště. Z těchto důvodů byl sestaven model úložiště ve tvaru kvádru a byla provedena předpověď průběhu teploty vystupujícího vzduchu. Byla zachována konstrukce tepelného jádra založená na konglomerátu granitových kostek a TVG. Tepelné jádro i s výměníkem bylo prodlouženo na délku 5 metrů, Identické 40cm topné tyče byly umístěny každý jeden běžný metr.

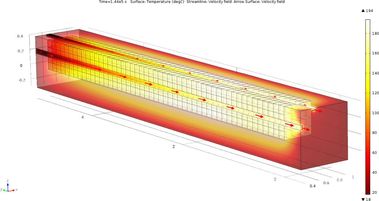
Obr. 8 Rozložení teplot v řezu tepelným úložištěm 20 hodin od počátku odběru

Simulace úložiště byla provedena na zjednodušené geometrii modelu (model neobsahuje rozdělovací a směšovací prvek vzduchotechniky). Ten byl z důvodů vysoké výpočetní náročnosti a zároveň malého vlivu na výsledek zanedbán. V modelu je uvažována symetrie ve dvou osách a tepelný transport je simulován pouze ¼ objemu úložiště (viz Obr. 8).

Vzhledem k liniovému charakteru a pravidelnému rozložení topných tyčí dochází k plnění úložiště se stejnou dynamikou jako v případě krychlového úložiště popsaného výše. Délka úložiště zajišťuje, že pokles teploty vystupujícího média je rozložen do delšího období oproti testovanému prototypu.

Ohřev úložiště byl simulován po dobu 24 hodin, odběr tepla následujících 168 hodin (7 dní) do úplného vyčerpání úložiště. Rychlost proudění v tepelném výměníku byla zadána shodně s předchozími simulacemi 4,5 m∙s⁻¹. Na levém grafu z Obr. 9 je zobrazen průběh simulované teploty vystupujícího vzduchu. Po zahájení odběru tepla z výměníku vystupuje vzduch s průměrnou teplotou 200 °C. Teplota 100 °C je podkročena až po 20 hodinách odběru. Další možnost regulace teploty vystupujícího média spočívá v regulaci rychlosti média v tělese výměníku.

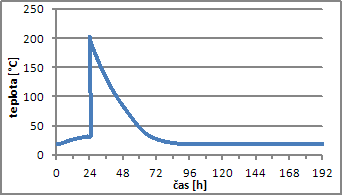
Obr. 9a Průběh teploty vystupujícího vzduchu

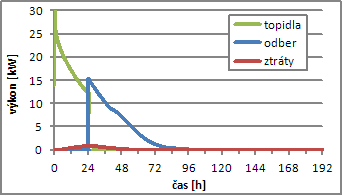Obr. 9b Průběh ztrát, dodaného a odebraného tepla

Obr. 9 Průběh teploty vystupujícího vzduchu (vlevo); průběh ztrát, dodaného a odebraného tepla (vpravo)

Úložiště na počátku plnění odebírá příkon přes 30 kW. Během 24 hodin dochází k jeho poklesu na 12 kW. Počáteční odebírané teplo odpovídá výkonu 15 kW a téměř lineárně, během 48 hodin odběru (24–72), klesá až k nule. Tepelné ztráty pláštěm ve špičce činí 1,1 kW. Uvedené hodnoty jsou přepočteny pro celou konstrukci úložiště. Během simulace bylo do úložiště doplněno 369 kWh tepla, z toho bylo následně odebráno 336 kWh. Celková ztráta pláštěm činila 33 kWh (9 %).

Poděkování

Tato práce vznikla v rámci výzkumného projektu „Reversibilní Skladování Energie“ podporovaného Technologickou agenturou České republiky v rámci projektu ALFA (ev. č. TA01020348).

Literatura

[1] Abedin A. H., Rosen M. A.: Assessment of a closed thermochemical energy storage using energy and exergy methods. Applied Energy 93, 18–23 (2012)
[2] COMSOL – Multiphysics Modeling and Simulation Software. Multiphysics Modeling and Simulation Software: 2013. Online 7. 5. 2014: http://www.comsol.com
[3] Cabeza L. F., Castellón C., Nogués M., Medrano M., Leppers R., Zubillaga O.: Use of microencapsulated PCM in concrete walls for energy savings, Energy and Buildings 39(2), 113–119 (2007). Online 7. 5. 2014:
http://web.ornl.gov/sci/buildings/2012/2007%20B10%20papers/035_Castellon.pdf
[4] Dunn R., Lovegrove K., Burgess G.: A Review of Ammonia-Based Thermochemical Energy Storage for Concentrating Solar Power, Proceedings of the IEEE 100(2), 391–400 (2012)
[5] Fernandes D., Pitié F., Cáceres G., Baeyens J.: Thermal energy storage: „How previous findings determine current research priorities“. Energy 39(1), 246–257 (2012)
[6] Fernandez A. I., Martínez M. , Segarra M., Martorell I., Cabeza L. F.: Selection of materials with potential in sensible thermal energy storage, Solar Energy Materials and Solar Cells 94(10), 1723-1729 (2010). Online 7. 5. 2014:
http://intraweb.stockton.edu/eyos/energy_studies/content/docs/effstock09/Session_4_1_High_Temperature_Applications/29.pdf
[7] Gil A., Medrano M. Martorell I., Lázaro A., Dolado P., Zalba B., Cabeza, L. F.: State of art on high temperature thermal energy storage for power generation. Part 1 – Concepts, materials and modelization. Renewable and Sustainable Energy Reviews 14(1),31–55 (2010)
[8] Gil A., Arce P., Martorell I., Medrano M., Cabeza, L. F: State of the art of high temperature storage in thermosolar plants (2009). Online 7. 5. 2014:
http://www.researchgate.net/profile/Luisa_F_Cabeza/publication/228519534_State_of_the_art_of_high_temperature_storage_in_thermosolar_plants/file/9c960520013951d6b7.pdf
[9] Kunc J.: Využití odpadního tepla při chlazení zimních stadionů. TZB-info.cz (2006) Online 7. 5. 2014:
http://www.tzb-info.cz/3325-vyuziti-odpadniho-tepla-pri-chlazeni-zimnich-stadionu
[10] Laing D., Steinmann W. D., Tamme R., Richter C.: Solid media thermal storage for parabolic trough power plants. Solar Energy, 80(10), 1283–1289. (2006)
[11] Medrano M., Gil A., Martorell I., Potau X., Cabeza L. F.: State of the art on high-temperature thermal energy storage for power generation. Part 2 — Case studies. Renewable and Sustainable Energy Reviews, 14(1), 56–72. (2010)
[12] Neveselý M.: Využití odpadního tepla v průmyslu pro vytápění tepelnými čerpadly. TZB-info.cz (2012) Online 7. 5. 2014:
http://www.tzb-info.cz/111449-vyuziti-odpadniho-tepla-v-prumyslu-pro-vytapeni-tepelnymi-cerpadly
[13] Orel V.: Akumulace tepelné energie při skupenských změnách látek. TZB-info.cz (2002). Online 7. 5. 2014:
http://www.tzb-info.cz/1005-akumulace-tepelne-energie-pri-skupenskych-zmenach-latek
[14] Py X., Calvet N., Echegut P., Bassada C., Olives R., Meffre A., Veron E., Ory S.: Recycled Material for Sensible Heat Based Thermal Energy Storage to be Used in Concentrated Solar Thermal Power Plants, Journal of Solar Energy Engineering 133(3), (2011).
[15] Py X., Calvet N., Olives R., Echegut P., Bassada C., Jay F.: Thermal storage for solar power plants based on low cost recycled material (2009). Online 7. 5. 2014:
http://www.researchgate.net/profile/Catherine_Bessada/publication/228474806_Thermal_storage_for_solar_power_plants_based_on_low_cost_recycled_material/file/5046351cd111911da4.pdf
[16] Rálek P., Hokr H.: Numerical Simulation of Temperature and Stress Fields in the Rock Heating Experiment, COMSOL Conference 2012 Milan Proceedings, COMSOL Inc., USA (2012). Online 7. 5. 2014:
http://www.comsol.com/offers/conference2012papers/papers/file/id/13245/file/13330_raalek_paper.pdf
[17] Reversibilní skladování energie. Online 7. 5. 2014: http://resen.cz
[18] Saeid S., Al-Khoury R., Barends F.: An efficient computational model for deep low-enthalpy geothermal systems, Computers & Geosciences 51, 400–409 (2013)
[19] Tamme R., Laing D., Steinmann W. D. Advanced Thermal Energy Storage Technology for Parabolic Trough, Journal of Solar Energy Engineering 126(2), 794–800 (2004)
[20] Tamme R., Laing D., Steinmann W. D.: Advanced Thermal Energy Storage Technology for Parabolic Trough.Proceedings of International Solar Energy Conference 2003. Online 7. 5. 2014:
http://www.jkearney.com/~dwk/TES_Papers/Tamme_Advanced_Storage.pdf
[21] Technická univerzita v Liberci, Tepelně vodivá hmota na bázi geopolymeru. Česká republika. Užitný vzor CZ 25908. 26. 9. 2013
[22] Wagner J.: Fotovoltaika a úložiště elektrické energie – největší témata konference Nekonvenční zdroje elektrické energie. TZB-info.cz (2012) Online 7. 5. 2014:
http://oze.tzb-info.cz/8679-fotovoltaika-a-uloziste-elektricke-energie-nejvetsi-temata-konference-nekonvencni-zdroje-elektricke-energie

English Synopsis

High temperature thermal energy storage with geopolymer

Surplus energy can be stored in the form of sensible heat. The present concept utilizes rock material and a thermally conductive geopolymer to construct the thermal energy storage with working temperatures up to 400 ° C. The paper describes a model evaluation of the performance impact of selected storage materials.