Nejnavštěvovanější odborný web
pro stavebnictví a technická zařízení budov

Vliv stagnačních stavů na solární soustavy

11.8.2014

Ing. Petr Kramoliš, doc. Ing. Mojmír VRTEK, Ph.D.

Recenzovaný

Příspěvek se zabývá popisem a modelováním stagnačních stavů v solárních kolektorech, kdy již nelze využít možný tepelný výkon kolektorů z důvodu přebytku produkovaného tepla. V těchto případech je jednou z možností zastavit průtok teplonosné látky a kolektory ponechat v klidovém stavu, kdy dojde k energetické rovnováze mezi tepelnými zisky kolektorů a jejich tepelnými ztrátami, případně i tepelnými ztrátami potrubní části soustavy navazující bezprostředně na kolektorové pole. Ve většině případů soustav s kvalitními solárními kolektory pak dochází v tomto stavu k vypařování teplonosné látky. Používané nemrznoucí směsi na bázi vodního roztoku propylenglykolu patří mezi tzv. zeotropní směsi, u kterých je teplotní průběh vypařování odlišný od vypařovacího děje čisté vody či jiných čistých látek. V příspěvku jsou popsány jak jednotlivé fáze této stagnace, tak je proveden rozbor chování soustav s různým poměrem objemu kolektorů a objemu expanzní nádoby.

Úvod

Se zvětšujícími se solárními soustavami, ať již v sítích místních CZT nebo v průmyslu, dochází k nárůstu kolektorové plochy. Při snížení či zastavení odběru tepla ze soustavy, eventuálně výpadku elektrické energie, nastává v době oslunění přehřívání solárních kolektorů na vysoké teploty, které snižují životnost zařízení i teplonosné kapaliny. Tento problém je nutno řešit vždy individuálně s ohledem na hydraulické zapojení nejen absorpční plochy, ale zvláště vzhledem k zapojení celého kolektorového pole a soustavy. Důležitou roli zde hraje schopnost vyprazdňování kolektorů a velikost expanzní nádoby [4]. Výsledky pomohou řešit v praktické rovině problémy spojené se stagnačními stavy.

Proces stagnace

Proces stagnace probíhá v 5 fázích [2], [5], [1], které jsou dále popsány:

Fáze 1 – Roztažení kapaliny

Při zastavení průtoku a zvýšení teploty zvětší kapalina svůj objem, začínají se tvořit první parní bubliny.

Fáze 2 – Vytlačení kapaliny z kolektoru prvním vytvořením páry

Zpočátku vznikající pára vytlačí velkou část horkého kapalného obsahu kolektoru do soustavy, a tím do expanzní nádoby pronikne také další kapalina, takže se tlak systému podstatně zvýší. Současně stoupá i teplota v kolektoru. Fáze 2 končí, když pára dosáhne k přípojce kolektoru. Pro další průběh je tato fáze rozhodující. Čím méně je kapaliny v kolektoru, tím méně páry se tvoří.

Fáze 3 – Vyprázdnění kolektoru – fáze s nasycenou párou

Pokud je později tímto způsobem kolektor prostupný pro páru, není již zbytková kapalina vyskytující se ještě v kolektoru vytlačována, ale musí se odpařit. Tato pára nyní může, podle míry jí přenášené energie, proniknout více nebo méně hluboko do soustavy a vtlačit další kapalinu do expanzní nádoby, tlak soustavy tak dále stoupá a dosahuje maximální hodnoty. Ve všech oblastech soustavy, kterých pára dosáhne, je dosaženo teplot, které odpovídají teplotě syté páry příslušného tlaku (přibližně 130 až 150 °C). Tlak v soustavě stoupá, dokud se nevyrovnají tepelné ztráty potrubí naplněného parou (event. chladiče, je-li v tomto potrubí zabudován) s parním výkonem kolektorů. Tento parní výkon je možno popsat měrným výkonem vztaženým na 1 m² apertury označovaným jako DPL (Dampfproduktionsleistung). Je závislý na množství páry a jejím termodynamickém stavu.

V nepříznivých případech může pára proniknout až k teplotně citlivým komponentám soustavy a poškodit je. V této fázi je dosaženo maximálního dosahu páry a většinou i maximálního objemu páry a maximálního tlaku v soustavě.

Fáze 4 – Vyprázdnění kolektoru – fáze s nasycenou párou a přehřátou párou

S přibývajícím odpařováním zbytkové kapaliny vysychá kolektor, je produkováno méně páry a kolektor se dále vyprazdňuje. Expanzní nádoba vtlačuje kapalinu zpět do soustavy a tlak klesá. Během toho, co je pára uvnitř suchého kolektoru přehřátá a absorbér může dosahovat podle záření teplot až nad 200 °C, klesají teploty nasycené páry mimo kolektor. Tento stav může trvat několik hodin.

Fáze 5 – Opětovné naplnění kolektoru

Teprve když se sluneční ozáření a tím i teploty v kolektoru dostatečně sníží, je také kolektor znovu naplněn kapalinou. Ukazatelem vyprazdňovací schopnosti kolektorů eventuálně polí je maximální parní výkon v době stagnace. Nejvyšší je na konci fáze 3.

U plochých kolektorů s dobrou schopností se vyprazdňovat dosahuje parní výkon 35 až 60 W/m² kolektorové plochy, u plochých kolektorů s nepříznivou schopností se vyprazdňovat 50 až 110 W/m². Při nižším tlaku v kolektorech výkon stoupá, při vyšším tlaku klesá (tlak určuje vypařovací teplotu a tím i solární zisk kolektoru při stagnaci). Při vysokých hodnotách tvorby páry může pára pronikat až do strojovny, pokud nejsou použity chladiče (vzduchové, odpařovací). Vakuové trubicové kolektory mohou dosahovat maximálního výkonu při tvorbě syté páry 180 až 200 W/m² kolektorové plochy.

Z tohoto popisu průběhu stavu stagnace je zřejmé, že množství zbytkové kapaliny, která zůstává v kolektoru na konci fáze 2, podstatně rozhoduje o jeho chování ve stavu stagnace. Kolektory, případně soustavy s dobrou schopností vyprazdňování vykazují velmi malé množství zbytkové kapaliny a tím i nepatrné dosahy páry. U těchto soustav probíhá proces stagnace bez problémů. Naproti tomu mohou nepříznivé schopnosti zařízení při vyprazdňování vést k vysokým dosahům páry s přehřátím komponent soustavy.

Vše o solárních termických soustavách na TZB-info

Teplota varu kapaliny

Teplotou varu kapaliny se zde rozumí teplota teplonosné látky v kolektoru, při které se začínají uvolňovat páry směsi vody a látky zabraňující tuhnutí pod bodem mrazu. Tato teplota má vliv na parní výkon kolektoru. Pro směs vody a propylenglykolu (dále PG) s hmotnostní koncentrací 40 % PG lze vypočíst teplotu podle vztahu

t_stag =100 + 35,1 ⋅ ln p_sys 100 (1) [°C]

kde je

p_sys: – absolutní tlak v soustavě v místě vypařování [kPa] [8].

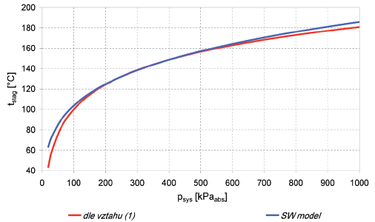
Obr. 1 Srovnání modelů pro stanovení teploty varu kapaliny v závislosti na absolutním tlaku

Srovnání průběhu teploty syté páry t_stag, který byl zpracován podle vztahu (1), a průběhu teploty vytvořeném v složitějším Wilsonově modelu (dále SW model), je vidět na obr. 1. Obě křivky se velmi dobře shodují v rozsahu absolutních tlaků 150 až 600 kPa, což znamená, že použití jednoduchého vztahu (1) je pro praktické výpočty v daném rozsahu dostatečně přesné.

Průběžným měřením teploty po délce přípojného potrubí lze zjistit dosah syté páry, tzn. čelo páry. Teplota páry je závislá na p_sys.

Teoretický výkon kolektoru při varu

Podle teploty varu kapaliny můžeme vypočítat teoretický výkon kolektoru při varu. Je to pouze výpočtová hodnota, která je potřebná pro stanovení reálných parametrů správného návrhu expanzní nádoby.

P_stag = G_T,stag ⋅ η₀ − a₁(t_stag − t_e) − a₂(t_stag − t_e)² (2) [W/m²]

kde je

P_stag: – teoretický výkon kolektoru při varu v okamžiku maximálního dosahu páry [W/m²]
G_T,stag: – celkové sluneční ozáření při stagnaci [W/m²]
t_stag: – teplota varu teplonosné látky [°C]
t_e: – teplota okolního vzduchu [°C]
η₀: – optická účinnost kolektoru [–]
a₁: – lineární součinitel tepelných ztrát [W/m²K]
a₂: – kvadratický součinitel tepelných ztrát [W/m²K²]

Pro srovnání byly stanoveny teoretické výkony při varu pro dva typy kolektorů s parametry uvedenými v tab. 1.

Tab. 1 Koeficienty účinnostních charakteristik srovnávaných kolektorů
	Kolektor A	Kolektor B
`η`₀ [–]	0,805	0,785
`a`₁ [W/m²K]	3,017	4,324
`a`₂ [W/m²K²]	0,005	0,009

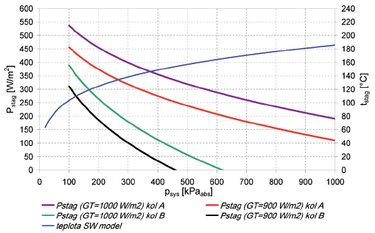
Obr. 2 Teoretické výkony při varu srovnávaných kolektorů pro dvě různá ozáření

Teoretické výkony při varu (viz obr. 2) byly pro oba kolektory vypočítány při dvou hodnotách celkového ozáření G_T = 900 W/m² a G_T = 1000 W/m². Křivka teploty ukazuje teplotu varu. Je patrné, že kvalita absorpčního povrchu a tepelně izolační vlastnosti výrazně ovlivňují dosažitelnou výši teploty varu a v důsledku pak i teoretický výkon při varu.

Výsledky publikované v [8] ukazují na nárůst tohoto výkonu u vakuových trubicových kolektorů, ale i vysoce selektivních plochých kolektorů. Zvýšení není lineární. Při měření na zkušebních polích kolektorů bylo zjištěno, že velké množství páry vzniká v kolektorech, ačkoli je stagnační výkon nulový. Důvodem tohoto rozporu je nesprávný předpoklad, že teplota kolektoru během stagnace odpovídá teplotě varu. Reálně tento předpoklad neplatí pro kolektory s nepříznivou schopností se vyprazdňovat, jelikož poměrně mnoho kapaliny zůstává v kolektoru a snižuje průměrnou teplotu teplonosné látky. Tím se zvyšuje účinnost kolektoru a dochází ke zvýšení tvorby syté páry oproti teoretickému předpokladu.

Vzhledem k tomu, že pro návrh solární soustavy je podstatný vytlačený objem tekutiny z potrubí do expanzní nádoby, je praktičtější sledovat parní výkon kolektoru (DPL).

Tab. 2 Tepelné ztráty potrubí při teplotním spádu 130/25 °C
DN	15	20	25	32	40	50
průměr/tloušťka stěny	18/1,0	22/1,0	28/1,5	35/1,5	42/1,5	54/1,5
součinitel tepelné vodivosti izolace [W/mK]	0,053	0,053	0,053	0,053	0,053	0,053
tloušťka izolace [mm]	20	20	30	30	40	50
součinitel prostupu tepla [W/m²K]	0,253	0,273	0,259	0,295	0,293	0,302
tepelná ztráta na 1 m [W/m]	26,6	28,7	27,2	31,0	30,8	31,7

Tab. 3 Tepelné ztráty potrubí při teplotním spádu 155/30 °C
DN	15	20	25	32	40	50
průměr/tloušťka stěny	18/1,0	22/1,0	28/1,5	35/1,5	42/1,5	54/1,5
součinitel tepelné vodivosti izolace [W/mK]	0,060	0,060	0,060	0,060	0,060	0,060
tloušťka izolace [mm]	20	20	30	30	40	50
součinitel prostupu tepla [W/m²K]	0,273	0,298	0,291	0,330	0,326	0,332
tepelná ztráta na 1 m [W/m]	34,1	37,3	36,4	41,3	40,8	41,5

Parní výkon kolektoru

Parní výkon kolektoru DPL zatím přesně vypočítat nelze, protože neumíme předem stanovit vyprazdňovací schopnost kolektoru a celého pole. Na zrealizované soustavě to však měřením zjistit lze.

Hodnota parního výkonu kolektoru vypovídá, kolik sluneční energie se spotřebuje na produkci páry směsi voda – PG. Parní výkon byl změřen na třech třídách kolektorů s různými vyprazdňovacími vlastnostmi. I když se nejedná o přesnou hodnotu, přesto pomáhá při návrhu soustav [8].

Empirické vztahy byly odvozeny z průběhu měření kolektorů. Pro střední třídu má vztah tvar

DPL = 0,2 ⋅ P_stag + 40 (3) [W/m²]

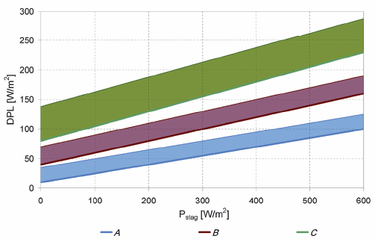
Obr. 3 Srovnání parního výkonu pro různé schopnosti vyprazdňování kolektorů

Jiná možnost je grafické zpracování pro tyto tři třídy podle změřených výkonů. Výsledky jsou zpracovány v grafu na obr. 3. Zelené pole představuje kolektory a zapojení se špatnou schopností vyprazdňování (C), modré pole (spodní) naopak nejlepší schopnost vyprazdňování (A). Spodní ohraničení každé plochy je střední hodnotou ze všech měření této třídy, horní čára pak vymezuje maximální hodnoty dosažené v dané třídě. Minimální hodnoty nejsou zobrazeny, neboť pro návrh solární soustavy nejsou podstatné.

Vypočteme-li teplotu při varu, z ní teoretický výkon při varu P_stag, pak již můžeme podle úrovně vyprazdňovacích schopností určit alespoň rozsah parního výkonu kolektoru DPL.

Objem páry v potrubí solární soustavy zjistíme snadno, vypočteme-li, jaká délka potrubí je zapotřebí pro odvedení tohoto tepla parního výkonu. Tepelné ztráty potrubí v závislosti na teplotě páry, okolní teplotě, průměru potrubí, tepelné vodivosti izolace a její tloušťce můžeme zjistit z tab. 2 a 3 [6]. Teplotní spád uvádí teplotu syté páry/teplota vzduchu okolo potrubí. Tepelné ztráty trubek nezávisí příliš na světlosti potrubí, ale na tloušťce izolace a jejím poměru k průměru trubky.

Takto stanovený objem páry v potrubí při maximálním dosahu je jiná hodnota než vytvořená pára v kolektoru. Je to proto, že značná část páry zkondenzuje v potrubí, zmenší se výrazně její objem, přičemž teplo je odváděno potrubím do okolního prostředí.

Měřením na zkušebních funkčních soustavách bylo ověřeno, že tvorba páry dosahuje tepelný výkon cca 30 až 90 W/m² kolektorové plochy, maximálně až 120 W/m². Tyto hodnoty způsobují, že pára dosáhne daleko od kolektorů, mnohdy až do strojovny. Orientačně je možno dosah určit podle dimenzí potrubí a předpokládaných teplot syté páry směsi vody a PG. Při běžných rozměrech trubek, izolace a teplotě par cca 150 až 160 °C jsou měrné tepelné ztráty potrubí cca 27 až 38 W/m. Kolektorové pole 100 m² může mít vývin páry cca 5 až 9 kW. Pro kondenzaci v potrubí je nutná délka cca 150 až 300 m. V případě velmi dobré vyprazdňovací schopnosti kolektoru to může být cca 75 až 120 m.

Vypařování směsi voda – propylenglykol

Směs vody a PG tvoří v běžných provozních podmínkách tzv. zeotropní směs. Tuto směs lze v krátkosti charakterizovat tak, že v průběhu vypařovacího izobarického procesu dochází ke zvyšování výparné teploty, to znamená, že pokud se v průběhu vypařování růst teploty zastaví, zastaví se i samotná tvorba páry.

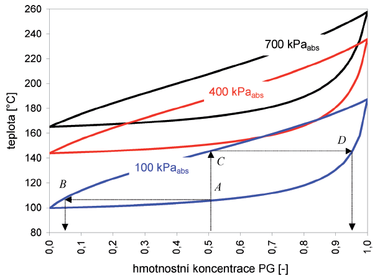
Obr. 4 Binární diagramy vypařování směsi voda – PG pro různé tlaky

Chování směsi během vypařování je možno znázornit v binárním diagramu teplota – koncentrace (obr. 4) zpracovaném na základě dat z SW modelu.

Jako příklad bude vysvětleno vypařování směsi o hmotnostní koncentraci propylenglykolu 51 % při konstantním absolutním tlaku 100 kPa (viz spodní část obr. 4). Dosáhne-li kapalina teploty odpovídající bodu A (stav vroucí kapaliny – cca 106 °C) začnou se z kapaliny vypuzovat páry směsi, které budou mít koncentraci odpovídající bodu B (cca 4 % PG). Jestliže kapalinu opustí páry bohatší na vodu, bude se kapalina s rostoucí teplotou postupně zahušťovat (po křivce A-D), přičemž se z ní budou odpařovat páry stále bohatší na PG, a tudíž se oproti výchozí koncentraci (4 %) budou také zahušťovat (po křivce B-C). Těsně před dosažením teploty bodu C (cca 145 °C) budou mít páry složení téměř odpovídající výchozí koncentraci 51 %, ale poslední „kapky“ kapaliny budou mít koncentraci bodu D. Při teplotě bodu C bude směs ve stavu syté páry již s původní koncentrací 51 %, nad touto teplotou pak bude ve stavu přehřáté páry. Oblast mezi teplotami bodu A a C je oblast mokré páry. Rozdílu teplot mezi začátkem a koncem vypařování (A-C) se někdy říká teplotní skluz. Na obrázku jsou pak naznačeny další zpracované křivky odpovídající vypařovacím tlakům 400 a 700 kPa.

U varianty s plochými kolektory byl měřením [8] zjištěn proces destilování teplonosné směsi voda – PG uvnitř pole. Po stagnaci bylo vidět na průhledítku u solární čerpadlové skupiny velmi světlé zabarvení, což ukazuje zvýšený podíl vody. Analýza tekutiny tuto domněnku potvrdila. Z analýzy a zvláště z binárního diagramu je vidět, že se při prvních fázích stagnace v kolektoru tvoří pára s vysokou koncentrací vody, která v potrubí opět kondenzuje. V kolektoru pak zůstává kapalina s vyšší koncentrací propylenglykolu.

Příčiny ovlivňující průběh stagnace

Na vyprazdňovací schopnost kolektorů při stagnaci má zásadní vliv vnitřní propojení trubiček absorbéru, které mají mít alespoň jednu přípojku ve spodní části. Rozhodující přitom je vytvoření tzv. kapalinových pytlů uvnitř kolektorového pole, což je nežádoucí. Kapalina nemůže odtéct a opustí kolektor pouze odpařením.

Dále je nutné pamatovat na celkové zapojení kolektorového pole. I kolektory s dobrou vyprazdňovací schopností, jsou-li nepříznivě zapojeny v kolektorovém poli (např. potrubí umístěné nad kolektory event. potrubní smyčky), vykazují nepříznivé vlastnosti. Hlavní příčinou je nevhodné propojení kolektorů, které pak při stagnaci zůstávají zaplněny kapalinou.

Základní principy pro vyprazdňování jednotlivých kolektorů musí být dodržovány také u kolektorových polí.

Obr. 5 Zapojení chladičů v primárním okruhu [2]

Vyprazdňování ovlivňuje taktéž umístění zpětné klapky u oběhového čerpadla. Brání-li klapka na výtlaku průniku tekutiny do expanzní nádoby, zůstává pak volné pouze výstupní potrubí z kolektoru. Tím se ovšem potrubní síť zmenší na polovinu, a proto pára snadno dosáhne až do strojovny. Kolektor zůstává při stagnaci zaplněn kapalinou a vytváří tak z kolektoru parní kotel, dokud se pára nestlačí a kapalina nezahustí natolik, až var ustane. Přehřívání tekutiny však pokračuje dál se všemi důsledky. Expanzní nádoba by měla být zapojena vůči zpětné klapce tak, aby do ní teplonosná tekutina mohla přitékat přívodním i zpětným potrubím solární soustavy (obr. 5).

Zapojení kolektoru má být takové, aby v době stagnace byly obě potrubí průchodné směrem z kolektoru ke strojovně. To usnadní odtok kapaliny a sníží tvorbu par na minimum.

Pokud nelze změnit vlastnosti kolektorů ani zapojení kolektorového pole (vliv stavebního řešení), je nutné využít pasivních nebo aktivních chladičů, které odvedou přebytečné solární teplo.

U realizovaných soustav byly statisticky zjišťovány příčiny stagnace [8]. Nejčastější příčinou stagnace nebyla vysoká teplota v zásobníku, jak se u kombinovaných soustav očekávalo, ale chyba regulace (cca z 60 %). Překročení povolené teploty v zásobníku bylo cca v 30 % případů. Stagnace, jejíž příčinou byl vznik netěsnosti v solárním okruhu, se vyskytla pouze cca v 10 % případů.

Rozsah platnosti

Výše uvedené výsledky vycházejí z měření zkušebních kolektorových polí do 30 m² a zrealizovaných zařízení v běžném provozu s aperturou do 90 m². Ukázalo se také, že se vzrůstající plochou kolektorů klesá množství vytvořené páry v přepočtu na m². Pro vytvoření prognózy pro větší pole než výše uvedené, je nutno počítat s nepřesností modelu představující 25 %.

Stagnační chladiče

Průzkum a posouzení testovaných polí ukázaly, že hydraulika kolektorových polí má rozhodující vliv na stagnační chování. Zvýšením systémového tlaku lze snížit tvorbu páry až o 50 %, ale zvýšená teplota pak více zatěžuje teplonosnou látku a další komponenty.

Při návrhu solární soustavy (při zpracování projektu) by se v každém případě mělo dbát na dobrou schopnost vyprazdňování kolektorového pole. Pokud to není možné, měly by být použity regulační strategie snižující zatížení, příp. osazeny stagnační chladiče odvádějící teplo páry. Chladicí provoz systému v době mimo sluneční svit, kdy je snaha odvést přes kolektory část naakumulovaného tepla do okolí, působí na snížení zatížení jen omezeně, zvláště u vakuových kolektorů.

Obr. 6 Zapojení pasivního chladiče do solární soustavy [7]

Pasivní chladiče (viz obr. 6) se umísťují před expanzní nádobu. Jejich účelem je nepropustit horkou páru do expanzní nádoby. Tvoří je žebrované trubky podobné jako u vzduchotechnických výměníků, pouze žebra jsou větší vzhledem k menší rychlosti proudícího vzduchu. Pro menší solární pole do cca 60 m² je použití chladičů bez pomocné energie výhodné. Aktivní chladiče spoléhají na pomocnou energii pro ventilátor nebo čerpadlo. Tato řešení vyžadují náhradní zdroj a nejsou předmětem tohoto příspěvku.

Obr. 7 Řízení stagnačních stavů s použitím odpařovacího vodního chladiče [7]

Velmi zajímavé a účinné řešení je prostřednictvím vodního odpařovacího chladiče. Jedná se o beztlakou nádobu, do které je ponořen trubkový vertikální parní chladič (obr. 7). Páry vznikající v kolektorovém poli, jež nestačí zkondenzovat v potrubí, jsou ještě před strojovnou odvedeny do chladiče, kde kondenzují. Předané teplo ohřeje vodní obsah beztlaké nádoby, eventuálně odpaří jeho část. Vodní pára volně odchází do venkovního prostředí, zkondenzovaná pára směsi vody a propylenglykolu se vrací do sběrné nádoby, odkud je později čerpadlem vrácena do solární soustavy. Odpařená voda se automaticky doplní z vodovodního řádu přímočinným ventilem. Podstatné na tomto řešení je, že nepotřebuje během stagnace žádnou externí energii, přičemž vodní obsah vystačí na několik period stagnace. Vhodnější je doplňování dešťovou vodou ze zásobní nádrže a pitnou vodu ponechat pouze jako rezervu.

Simulace stavu směsi voda – PG během vypařování v kolektoru

Simulace má za úkol rámcově popsat především základní chování směsi během vypařování, nerespektuje se zde, že vytlačená tekutina z kolektoru bude ochlazována okolním prostředím. Z toho důvodu lze níže uvedené výsledky chápat jako teoreticky mezní. V reálné soustavě bude docházet díky sdílení tepla do okolí v potrubí k vytvoření teplotního gradientu ve vytlačované tekutině, a tedy skutečný dosah páry nebude zdaleka takový.

Pro simulaci byla uvažována solární soustava, která má kolektorové pole o činném objemu 100 litrů a je naplněna 51% směsí PG a vody. V celé soustavě se předpokládá stejný tlak, není zde uvažováno s hydrostatickým tlakem, tzn. předpokládá se, jakoby expanzní nádoba a pojistný ventil byly na stejné výškové úrovni jako kolektorové pole. Výchozí stav soustavy je definován absolutním tlakem 400 kPa při ustálené teplotě 20 °C. Simulace je zpracována pro několik velikostí expanzní nádoby, která je zde definována objemem dusíku uzavřeném v nádobě při výše uvedeném stavu v soustavě 400 kPa a 20 °C. Byly zvoleny velikosti 200, 300, 400 litrů a jako extrém byla přidána nádoba s objemem 1000 litrů. Vzhledem k tomu, že díky vodní předloze vyplňuje dusík zpravidla cca ¾ celkového objemu nádoby, budou fyzické objemy nádob (oproti zde definovaným) o vodní předlohu větší.

Obr. 8 Průběh tlaku v soustavě v závislosti na teplotě pro různé velikosti expanzních nádob

Obr. 9 Průběh zvětšení objemu tekutiny a páry v soustavě v závislosti na teplotě pro různé velikosti expanzních nádob

Dále se předpokládá, že kapalina v potrubí mezi kolektorovým polem a expanzní nádobou se chová pouze jako píst a lze tudíž předpokládat, že součet objemu kolektorového pole a objemu expanzní nádoby je při všech stavech konstantní. Při simulaci byl využit dříve zmíněný SW model pro chování binárních směsí.

Simulace vychází z postupného zvyšování teploty stagnujícího kolektorového pole (s předpokladem rovnoměrně rozložené teploty), přičemž se v kolektorech kapalina s původním objemem 100 litrů rozpíná na úkor objemu dusíku v expanzní nádobě. To vede ke zvyšování tlaku v soustavě. Kromě růstu tlaku byla v modelu sledována teplota, kdy se začne směs vypařovat, dále pak celkový nárůst objemu uzavřené tekutiny a objem vytvořené páry, přičemž se uvažuje, že nedochází k ochlazení vytlačené tekutiny. Simulace byla ukončena při dosažení tlaku 700 kPa, po jehož překročení se předpokládá otevření pojistného ventilu s odvedením části teplonosné tekutiny mimo soustavu.

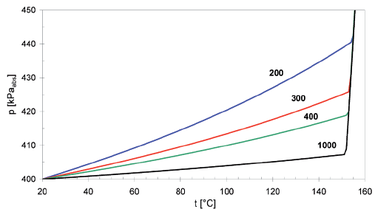
Na obr. 8 znázorněný průběh tlaků ukazuje, že u větších nádob nastane vypařování o něco dříve (bod prudkého nárůstu tlaku), neboť je v soustavě při dané teplotě nižší tlak. Jakmile však dojde v kolektoru k tvorbě páry, tak de facto tlak roste téměř nezávisle na velikosti expanzní nádoby.

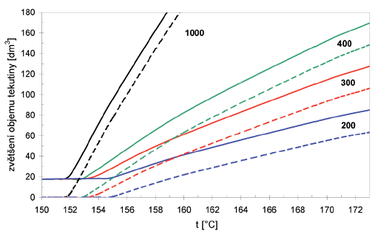
Obr. 9 ukazuje o kolik se zvětší celkový objem tekutiny (tj. nad rámec objemu 100 litrů kolektorového pole) a páry během ohřevu. Horní plná čára z dvojice čar stejné barvy znamená nárůst celkového objemu tekutiny, tzn. kapaliny případně i páry dohromady, spodní čára pak pouze zvětšení objemu páry. Jelikož je výchozí stav páry nulový, znázorňuje spodní čára objem páry v soustavě. Číselně jsou výsledky simulace shrnuty v tab. 4.

Tab. 4 Srovnání základních výsledků simulace stagnace pro různé velikosti expanzní nádoby
Expanzní nádoba [dm³]	200	300	400	1000
Začátek varu – teplota [°C]	155	154	153	152
Začátek varu – tlak [kPa]	443	431	420	409
700 kPa – teplota [°C]	173,3	173,3	173,4	173,5
700 kPa – zvětšení objemu tekutiny [dm³]	85,8	128,5	171,7	428,2
- z toho pára [dm³]	64,1	107,1	150,6	408,7
- z toho kapalina [dm³]	21,7	21,4	21,2	19,5

Výsledky v tabulce ukazují zajímavou skutečnost, že k otevření pojistného ventilu dojde ve všech srovnávaných případech skoro při stejné teplotě, což vyplývá i z téměř shodných strmých průběhů závislosti tlaku na teplotě za body počátků varu viz obr. 8. Na první pohled by se mohlo zdát, že soustavy s menšími nádobami budou lepší, neboť u nich bude docházet k menším změnám objemu a vývinu páry, avšak není tomu tak.

V prvé řadě je si nutno uvědomit, že pro vývin páry je potřeba dodat výparné teplo, které je mnohem větší než citelné teplo kapaliny. Jak bylo naznačeno na obr. 4, první vzniklé páry budou mít malou koncentraci PG (pod 10 %), lze tedy říci, že budou mít měrné výparné teplo řádově se blížící čisté vodě, tedy okolo 2 MJ/kg. Naproti tomu měrná tepelná kapacita kapaliny s uvažovanou koncentrací (51 % PG) se bude pohybovat kolem 0,4 MJ/(kg.K). Dojde-li u soustavy s větší nádobou k varu, bude schopna absorbovat větší množství tepla než soustava, u které zatím k varu nedošlo. To znamená, že při uvažovaném konstantním solárním příkonu bude teplota kolektorového pole s varem kapaliny růst v čase pomaleji než teplota soustavy naplněné pouze kapalinou. Ale i když v obou soustavách již dojde k vývinu páry, bude při dané teplotě soustava s větší nádobou schopna pojmout větší množství tepla – např. pro teplotu cca 160 °C bude u expanzní nádoby 1000 litrů vyvinuto 180 dm³ páry, kdežto pro 200litrovou nádobu pouze 20 dm³ páry (obr. 9).

Výsledky týkající se zvětšení objemu ukazují, zda se i při dobré vyprazdňovací schopnosti kolektorového pole s fyzickým objemem 100 litrů může dostat do potrubí pára. Zatímco u 200 litrové nádoby je navýšení objemu parou těsně před otevřením pojistného ventilu jen 64,1 dm³, to znamená, že veškerá vyvinutá pára má možnost zůstat v kolektorech, u 300litrové nádoby je již 7 dm³ páry vytlačeno z kolektorového pole. Vezme-li se nyní v úvahu reálný děj v potrubí, kde dochází (i přes izolaci) k ochlazování vytěsněné tekutiny (páry či kapaliny) okolním vzduchem, bude při sdílení tepla do okolí pára ochlazována a kondenzována. Nelze tudíž v praxi uvažovat, že teoretické dosahy páry mimo kolektory budou na úrovni výsledků pro 400 resp. 1000litrovou expanzní nádobu, tj. vytlačení cca 50,6 resp. 308,7 dm³ a je nutno tyto hodnoty považovat, jak již bylo uvedeno, za teoreticky mezní. Odpovídající množství páry ale muselo v kolektorech vzniknout.

Závěr

Rozvoj kombinovaných soustav a velkoplošných soustav přináší nutnost racionálního řešení stagnačních stavů. Jedním z prvních kroků je volba správného kolektoru s hydraulickým zapojením majícím schopnost dobrého vyprázdnění. Dalším krokem je sestavení kolektorů do polí tak, aby bylo opět umožněno co nejlepší vyprázdnění. Z uvedených faktů je patrno, že v mnoha případech bude nutné realizovat chladiče, v lepším případě dimenzovat expanzní nádobu na větší objemy než je běžně zvykem. Pro správný návrh expanzní nádoby je nutno provést výpočet dosahu páry v potrubí, který výsledný objem expanzní nádoby zásadně ovlivňuje.

Poděkování

Článek byl zpracován s laskavou podporou projektu ENET – Energetické jednotky pro využití netradičních zdrojů energie (CZ.1.05/2.1.00/03.0069).

Použité zdroje

[1] Matuška, T. Problematika stagnace solárních tepelných soustav. In: TZBinfo [online]. 14. 8. 2006. Dostupné z: http://www.tzb-info.cz/3462-problematika-stagnace-u-solarnich-tepelnych-soustav-i
[2] Hausner, R., Fink, C. Stagnation behaviour of solar thermal systems. Report of IEA SHC – Task 26 Solar Combi-systems, November 2002
[3] Streicher, W. Minimising the risk of water hammer and other problem at the beginning of stagnation of solar thermal plants – a theroretical approach. Solar energy. Vol 69. s. 187-196, 2001. ISSN 0038-092X
[4] Matuška, T. Solární tepelné soustavy, sešit projektanta 1. Pracovní podklady STP. Praha: Český svaz vědeckotechnických společností, 2009. ISBN 978-80-02-02186-5
[5] Fink, C., Riva, R. Solarunter – stütze Warmenetze im GeschoSSwohneban. AEE INTEC, AEE GMBH Gleisdorf, 1 Auflage, 2004
[6] Kramoliš, P., Vrtek, M. Řešení stagnačních stavů solárních soustav. Topenářství, instalace. 2008, č. 1, s. 46-51. ISSN 1211-0906
[7] Hausner, R., Fink, C., Kaiser, A., Stelzer, R. Stagnation of Large Scale Solar Plants. In: Proceedings of the EuroSun 2010. Graz
[8] Scheuren, J., Eisenmann, W. Stagnationsuntersuchungen in den Kollektorkreisen hochdimensionierter großer thermischer Solaranlagen. Institut für Solarenergieforschung Hameln (ISFH), 2007

English Synopsis

Stagnancy Situation Effect to Solar Systems

Authors are engaged in the description and modeling of stagnancy situations in solar collectors when the possible output of heat from collectors cannot be utilized due to the excess of the produced heat, in their contribution. One of possibilities in such events is to shut the flow of the heat transfer medium and to let collectors in the stagnation when the energy balance between collector heat gains and their losses occur; eventually heat losses of the system pipelines linked directly to the collector field. In this situation in most of cases in systems equipped with quality solar collectors occurs the evaporation of the heat transfer medium. Used anti-freeze mixtures established on the basis of water solution of propylene glycol fall to so called zeotropic mixtures that have the evaporation temperature process different from the evaporation process of pure water or other pure matters. Authors describe both individual phases of this stagnation and behavior analysis of systems with the different ratio of the capacity of collectors and the expansion vessel, in their contribution.